Modelspace - Demo 06¶
Objective¶
Learn about modelspace Modelspace.
Demo 06¶
How to Execute¶
Load src/modelviewprojection/demo06.py in Spyder and hit the play button.
Move the Paddles using the Keyboard¶
Keyboard Input |
Action |
|---|---|
w |
Move Left Paddle Up |
s |
Move Left Paddle Down |
k |
Move Right Paddle Down |
i |
Move Right Paddle Up |
Modelspace¶
NDC are not a natural system of numbers for use by humans. Imagine that the paddles in the previous chapters exist in real life, and are 2 meters wide and 6 meters tall. The graphics programmer should be able to use those numbers directly; they shouldn’t have to manually transform the distances into NDC.
Whatever a convenient numbering system is (i.e. coordinate system) for modeling objects is called modelspace. Since a paddle has four corners, which corner should be at the origin (0,0)? If you don’t already know what you want at the origin, then none of the corners should be; instead put the center of the object at the origin (Because by putting the center of the object at the origin, scaling and rotating the object are trivial, as shown in later chapters).
Representing a Paddle using Modelspace¶
modelspace - the coordinate system (origin plus axes), in which some object’s vertices are defined.
WorldSpace¶
WorldSpace is a top-level space, independent of NDC, that we choose to use. It is arbitrary. If you were to model a racetrack for a racing game, the origin of WorldSpace may be the center of that racetrack. If you were modeling our solar system, the center of the sun could be the origin of “WorldSpace”. I personally would put the center of our flat earth at the origin, but reasonable people can disagree.
For our demo with paddles, the author arbitrarily defines the WorldSpace to be 20 units wide, 20 units tall, with the origin at the center.
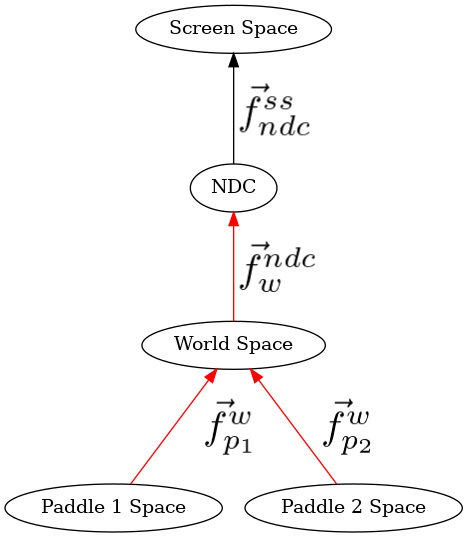
Demo 06¶
Modelspace to WorldSpace¶
The author prefers to view transformations as changes to the graph paper, as compared to view transformations as changes to points.
As such, for placing paddle1, we can view the translation as a change to the graph paper relative to world space coordinates (only incidentally bringing the vertices along with it) and then resetting the graph paper (i.e. both origin and axes) back to its original position and orientation. Although we will think of the paddle’s vertices as relative to its own space (i.e. -1 to 1 horizontally, -3 to 3 vertically), we will not look at the numbers of what they are in world space coordinates, as doing so
Will not give us any insight
Will distract us from thinking clearly about what’s happening
As an example, figure out the world space coordinate of the upper rights corner of the paddle after it has been translated, and ask yourself what that means and what insight did you gain?
The animation above shows multiple steps, shown now without animation.
Modelspace of Paddle 1¶
Paddle 1’s Modelspace¶
Vector |
Coordinates |
|---|---|
a |
(1,3) |
b |
(-1,3) |
c |
(-1,-3) |
d |
(1,-3) |
Modelspace of Paddle 1 Superimposed on Worldspace after the translation¶
Paddle 1’s graph paper gets translated -9 units in the x direction, and some number of units in the y direction, 0 during the first frame, based off of user input. The origin is translated, and the graph paper comes with it, onto which you can plot the vertices. Notice that the coordinate system labels below the plot and to the left of the plot is unchanged. That is world space, which has not changed.
Paddle 1’s Modelspace Superimposed on World Space¶
Vector |
Coordinates (modelspace) |
Coordinates (worldspace) |
|---|---|---|
a |
(1,3) |
(1,3) + (9,3) = (-8,5) |
b |
(-1,3) |
(-1,3) + (9,3) = (-10,5) |
c |
(-1,-3) |
(-1,-3) + (9,3) = (-10,-1) |
d |
(1,-3) |
(1,-3) + (9,3) = (-8,-1) |
Paddle 1’s vertices in WorldSpace Coordinates¶
Paddle 1’s Vertices in World Space.¶
Vector |
Coordinates (worldspace) |
|---|---|
a |
(-8,5) |
b |
(-10,5) |
c |
(-10,-1) |
d |
(-8,-1) |
Now that the transformation has happened, the vertices are all in world space. You could calculate their values in world space, but that will not give you any insight. The only numbers that matter for insight as that the entire graph paper of modelspace, which originally was the same as world space, has changed, bringing the vertices along with it.
Same goes for Paddle 2’s modelspace, relative to its translation, which are different values.
Modelspace of Paddle 2¶
Paddle 2’s Modelspace¶
Vector |
Coordinates |
|---|---|
a |
(1,3) |
b |
(-1,3) |
c |
(-1,-3) |
d |
(1,-3) |
Modelspace of Paddle 2 Superimposed on Worldspace after the translation¶
Paddle 2’s Modelspace Superimposed on World Space¶
Vector |
Coordinates (modelspace) |
Coordinates (worldspace) |
|---|---|---|
a |
(1,3) |
(1,3) + (9,-4) = (10,-1) |
b |
(-1,3) |
(-1,3) + (9,-4) = (8,-1) |
c |
(-1,-3) |
(-1,-3) + (9,-4) = (8,-7) |
d |
(1,-3) |
(1,-3) + (9,-4) = (10,-7) |
Paddle 2’s vertices in WorldSpace Coordinates¶
Paddle 2’s Vertices in World Space.¶
Vector |
Coordinates (worldspace) |
|---|---|
a |
(10,-1) |
b |
(8,-1) |
c |
(8,-7) |
d |
(10,-7) |
Scaling¶
Our paddles are now well outside of NDC, and as such, they would not be displayed, as they would be clipped out. Their values are outside of -1.0 to 1.0. All we will need to do to convert them from world space to NDC is divide each component, x and y, by 10.
As a demonstration of how scaling works, let’s make an object’s width twice as large, and height three times as large. (The author tried doing the actual scaling of 1/10 in an animated gif, and it looked awful, therefore a different scaling gif is showed here, but the concept is the same).
We can expand or shrink the size of an object by “scale”ing each component of the vertices by some coefficient.
Modelspace¶
Modelspace Superimposed on World Space¶
Worldspace. Don’t concern yourself with what the numbers are.¶
Our global space is -10 to 10 in both dimensions, and to get it into NDC, we need to scale by dividing by 10

Demo 06¶
where x_p1, y_p1 are the modelspace coordinates of the paddle’s vertices, and where p1_center_x_worldspace, p1_center_y_worldspace, are the offset from the world space’s origin to the center of the paddle, i.e. the translation.
Now, the coordinates for paddle 1 and for paddle 2 are in world space, and we need the match to take any world space coordinates and convert them to NDC.
Modelviewprojection comes with a math library, the 2D version is named “mathutils.py”. The main class in this module is “Vector2D”, which has two components: and x value, and a y value. To add a vector2d to another one on the right hand side of the ‘+’ symbol, we just add the respective components together, and create a new Vector2D.
557@dataclasses.dataclass
558class Vector1D(Vector):
559 x: float #: The value of the 1D Vector
In a Python class, we can overload the ‘+’ symbol, to make
objects addable, by implementing the __add__
method. The definition is just saying pairwise add each component.
Don’t stress about understanding the implementation, look at the
tests listed after.
67 def __add__(self, rhs: typing.Self) -> typing.Self:
96 if type(self) is not type(rhs):
97 return NotImplemented
98 return type(self)(
99 *[
100 a + b
101 for a, b in zip(
102 dataclasses.astuple(self), dataclasses.astuple(rhs)
103 )
104 ]
105 )
We can also model the opposite procedure, subtraction,
by implementing the __sub__
method.
158 def __sub__(self, rhs: typing.Self) -> typing.Self:
173 return self + -rhs
In our graphics code, instead of using “a+b”, we’ll use a more descriptive
name: “translate”, which is implemented using the addition symbol. But a few
things to note, translate
is a function on the mathutils module, not a method
on Vector2D class, and it’s wrapped in a class named
InvertibleFunction.
522def translate(b: Vector) -> InvertibleFunction:
523 def f(vector: Vector) -> Vector:
524 return vector + b
525
526 def f_inv(vector: Vector) -> Vector:
527 return vector - b
528
529 values = dataclasses.astuple(b)
530 tex_str: str = (
531 f"T_{{<[{str(values[0]) if len(values) == 1 else str(values)[1:-1]}]>}}"
532 )
533 negative_values = dataclasses.astuple(-b)
534 inv_str: str = f"T_{{<[{str(negative_values[0]) if len(negative_values) == 1 else str(negative_values)[1:-1]}]>}}"
535 return InvertibleFunction(f, f_inv, tex_str, inv_str)
Notice in particular that the “b” parameter is passed as an argument to “translate”, but the function for translating, named “f”, and the inverse of “f” named “f_inv”, take a Vector2D. This is because we will be translating many Vector2Ds using the same amount.
Invertible functions are stored in pairs, with the “active” function
being the first one passed to the constructor. So for translate above,
the adding of the Vector2Ds will be the function, but
InvertibleFunction
holds onto the second function, for later use to be able to undo the function’s
application.
67def test__vec1_translate():
68 fn: mu.InvertibleFunction = mu.translate(mu.Vector1D(2))
69 fn_inv: mu.InvertibleFunction = mu.inverse(fn)
70
71 input_output_pairs = [
72 [-3, -1],
73 [-2, 0],
74 [-1, 1],
75 [0, 2],
76 [1, 3],
77 [2, 4],
78 [3, 5],
79 [4, 6],
80 ]
81 for input_val, output_val in input_output_pairs:
82 wrap_vec1_test(fn, input_val, output_val)
83 wrap_vec1_test(fn_inv, output_val, input_val)
84
85
The above is a unit test that shows how the translate function can be used.
We call “translate”, a function which takes a translate amount, both in the x
direction and the y direction, but we have not yet specified what needs to be translated
by that amount. “translate” returns an
InvertibleFunction, which is
Callable[Vector2D, Vector2D]. Callable[Vector2D, Vector2D] is a type which
is a function that takes a Vector2D as input, and returns a Vector2D (in this case,
the output is the input, translated by Vector2D(x=2.0, y=3.0).
On the next 3 lines, we call the function t, passing in a Vector2D to be translated, and we test if the result is equal to the specified amount. (“approx”, is a function from the pytest module, which when tested for equality, returns true if the two floating point numbers under comparison are “close enough”).
We then define a function t_inv, by calling “inverse” on function “t”. We then see that composing t_inv and t results in no transformation.
Here’s how InvertibleFunction is implemented:
208@dataclasses.dataclass
209class InvertibleFunction:
219 func: typing.Callable[[Vector], Vector] #: The wrapped function
220 inverse: typing.Callable[
221 [Vector], Vector
222 ] #: The inverse of the wrapped function
223 latex_repr: str #: The LaTeX representation of the function
224 latex_repr_inv: str #: The LaTeX representation of the inverse function
Just as Python allows an object to override the ‘+’ and ‘-’ syntax,
in Python, any object can be treated as a function, by implementing the
__call__
method.
228 def __call__(self, x: Vector) -> Vector:
261 return self.func(x)
We can get the inverse of the procedure by the following
inverse, procedure
304def inverse(f: InvertibleFunction) -> InvertibleFunction:
335 return InvertibleFunction(f.inverse, f.func, f.latex_repr_inv, f.latex_repr)
Back to method’s on the Vector2D class. We can also define scaling of a Vector2D,
by implementing multiplication of Vector2D’s by a scalar, meaning a real number
that scaled the Vector2D by the same amount in all directions. We do this
by implementing the __mul__
and __rmul__ methods, where __rmul__ just means
that this object is on the right hand side of the multiplication.
109 def __mul__(self, scalar: float) -> typing.Self:
135 return type(self)(*[scalar * a for a in dataclasses.astuple(self)])
Just like we made a top level invertible function called “translate” for addition,
we are going to do the same for multiplication, and call it “uniform_scale”.
Notice in particular that the scalar is passed as an argument to
uniform_scale,
but the function for scaling “f”, and the inverse of “f” named “f_inv”, take a Vector2D.
This is because we will be scaling many Vector2Ds using the same scaling factor.
540def uniform_scale(m: float) -> InvertibleFunction:
541 def f(vector: Vector) -> Vector:
542 return vector * m
543
544 def f_inv(vector: Vector) -> Vector:
545 if m == 0.0:
546 raise ValueError("Not invertible. Scaling factor cannot be zero.")
547
548 return vector * (1.0 / m)
549
550 tex_str: str = f"S_{{{m}}}"
551 inv_str: str = f"S_{{{-m}}}"
552 return InvertibleFunction(f, f_inv, tex_str, inv_str)
NEW – Add the ability to scale a vector, to stretch or to shrink
94paddle1: Paddle = Paddle(
95 vertices=[
96 mu2d.Vector2D(x=-1.0, y=-3.0),
97 mu2d.Vector2D(x=1.0, y=-3.0),
98 mu2d.Vector2D(x=1.0, y=3.0),
99 mu2d.Vector2D(x=-1.0, y=3.0),
100 ],
101 color=colorutils.Color3(r=0.578123, g=0.0, b=1.0),
102 position=mu2d.Vector2D(-9.0, 0.0),
103)
104
105paddle2: Paddle = Paddle(
106 vertices=[
107 mu2d.Vector2D(x=-1.0, y=-3.0),
108 mu2d.Vector2D(x=1.0, y=-3.0),
109 mu2d.Vector2D(x=1.0, y=3.0),
110 mu2d.Vector2D(x=-1.0, y=3.0),
111 ],
112 color=colorutils.Color3(r=1.0, g=1.0, b=0.0),
113 position=mu2d.Vector2D(9.0, 0.0),
114)
paddles are using modelspace coordinates instead of NDC
119def handle_movement_of_paddles() -> None:
120 global paddle1, paddle2
121
122 if glfw.get_key(window, glfw.KEY_S) == glfw.PRESS:
123 paddle1.position.y -= 1.0
124 if glfw.get_key(window, glfw.KEY_W) == glfw.PRESS:
125 paddle1.position.y += 1.0
126 if glfw.get_key(window, glfw.KEY_K) == glfw.PRESS:
127 paddle2.position.y -= 1.0
128 if glfw.get_key(window, glfw.KEY_I) == glfw.PRESS:
129 paddle2.position.y += 1.0
130
131
Movement code needs to happen in modelspace’s units.
Code¶
The Event Loop¶
139while not glfw.window_should_close(window):
140 while (
141 glfw.get_time()
142 < time_at_beginning_of_previous_frame + 1.0 / TARGET_FRAMERATE
143 ):
144 pass
145 time_at_beginning_of_previous_frame = glfw.get_time()
146
147 glfw.poll_events()
148
149 width, height = glfw.get_framebuffer_size(window)
150 GL.glViewport(0, 0, width, height)
151 GL.glClear(sum([GL.GL_COLOR_BUFFER_BIT, GL.GL_DEPTH_BUFFER_BIT]))
152
153 draw_in_square_viewport()
154 handle_movement_of_paddles()
Rendering Paddle 1¶
158 GL.glColor3f(*iter(paddle1.color))
159
160 world_space_to_ndc: mu2d.InvertibleFunction = S(1.0 / 10.0)
161 p1_space_to_world_space: mu2d.InvertibleFunction = T(paddle1.position)
162 p1_to_ndc: mu2d.InvertibleFunction = (
163 world_space_to_ndc @ p1_space_to_world_space
164 )
165 GL.glBegin(GL.GL_QUADS)
166 for p1_v_ms in paddle1.vertices:
167 paddle1_vector_ndc: mu2d.Vector = p1_to_ndc(p1_v_ms)
168 GL.glVertex2f(paddle1_vector_ndc.x, paddle1_vector_ndc.y)
169
170 GL.glEnd()
Paddle 1’s Modelspace¶
Paddle 1’s Modelspace Superimposed on World Space¶
Reset coordinate system.¶
The coordinate system now resets back to the coordinate system specified on the left and below. Now, we must scale everything by 1/10. I have not included a picture of that here. Scaling happens relative to the origin, so the picture would be the same, just with different labels on the bottom and on the left.
Rendering Paddle 2¶
174 GL.glColor3f(*iter(paddle2.color))
175
176 world_space_to_ndc: mu2d.InvertibleFunction = S(1.0 / 10.0)
177 p2_space_to_world_space: mu2d.InvertibleFunction = T(paddle2.position)
178 p2_to_ndc: mu2d.InvertibleFunction = (
179 world_space_to_ndc @ p2_space_to_world_space
180 )
181 GL.glBegin(GL.GL_QUADS)
182 for p2_v_ms in paddle2.vertices:
183 paddle2_vector_ndc: mu2d.Vector = p2_to_ndc(p2_v_ms)
184 GL.glVertex2f(paddle2_vector_ndc.x, paddle2_vector_ndc.y)
185 GL.glEnd()
Paddle 2’s Modelspace¶
Paddle 2’s Modelspace Superimposed on World Space¶
Reset coordinate system.¶
The coordinate system is reset. Now scale everything by 1/10. I have not included a picture of that here. Scaling happens relative to the origin, so the picture would be the same, just with different labels on the bottom and on the left.
190 glfw.swap_buffers(window)