Rotation Fix Attempt 1 - Demo 08¶

Objective¶

Fix the rotation problem from the previous demo in a seemingly intuitive way, but do it inelegantly.

How to Execute¶

Load src/modelviewprojection/demo08.py in Spyder and hit the play button.

Move the Paddles using the Keyboard¶

Keyboard Input	Action
w	Move Left Paddle Up
s	Move Left Paddle Down
k	Move Right Paddle Down
i	Move Right Paddle Up
d	Increase Left Paddle’s Rotation
a	Decrease Left Paddle’s Rotation
l	Increase Right Paddle’s Rotation
j	Decrease Right Paddle’s Rotation

Description¶

The problem in the last demo is that all rotations happen relative to World Space’s (0,0) and axes. By translating our paddles to their position before rotating, they are rotated around World Space’s origin, instead of being rotated around their modelspace’s center.

In this demo, we try to solve the problem by making a method to rotate around a given point in world space, in this case, the paddle’s center.

src/modelviewprojection/mathutils2d.py¶

@dataclasses.dataclass
class Vector2D(mu1d.Vector1D):
    y: float  #: The y-component of the 2D Vector

src/modelviewprojection/mathutils2d.py¶

def rotate_around(
    angle_in_radians: float, center: Vector2D
) -> mu.InvertibleFunction[Vector2D]:
    return mu.compose(
        [mu.translate(center), rotate(angle_in_radians), mu.translate(-center)]
    )

Within the event loop, this seems quite reasonable

src/modelviewprojection/demo08.py¶

while not glfw.window_should_close(window):

src/modelviewprojection/demo08.py¶

    GL.glColor3f(*iter(paddle1.color))

    GL.glBegin(GL.GL_QUADS)
    rotatePoint: mu2d.Vector2D = paddle1.position
    for p1_v_ms in paddle1.vertices:
        fn: mu.InvertibleFunction[mu2d.Vector2D] = mu.compose(
            [
                mu.uniform_scale(1.0 / 10.0),
                mu2d.rotate_around(paddle1.rotation, rotatePoint),
                mu.translate(paddle1.position),
            ]
        )
        paddle1_vector_ndc: mu2d.Vector2D = fn(p1_v_ms)
        GL.glVertex2f(paddle1_vector_ndc.x, paddle1_vector_ndc.y)

src/modelviewprojection/demo08.py¶

    # draw paddle 2
    GL.glColor3f(*iter(paddle2.color))

    GL.glBegin(GL.GL_QUADS)
    rotatePoint: mu2d.Vector2D = paddle2.position
    for p2_v_ms in paddle2.vertices:
        fn: mu.InvertibleFunction[mu2d.Vector2D] = mu.compose(
            [
                mu.uniform_scale(1.0 / 10.0),
                mu2d.rotate_around(paddle2.rotation, rotatePoint),
                mu.translate(paddle2.position),
            ]
        )
        paddle2_vector_ndc: mu2d.Vector2D = fn(p2_v_ms)
        GL.glVertex2f(paddle2_vector_ndc.x, paddle2_vector_ndc.y)
    GL.glEnd()

All we did was add a rotate around method, and call it, with the paddle’s center as the rotate point.

Although this works for now and looks like decent code, this is extremely sloppy, and not thought out well at all. We apply a transformation from paddle space to world space, then do the inverse, then rotate, and then do the first transformation from paddle space to world space again.

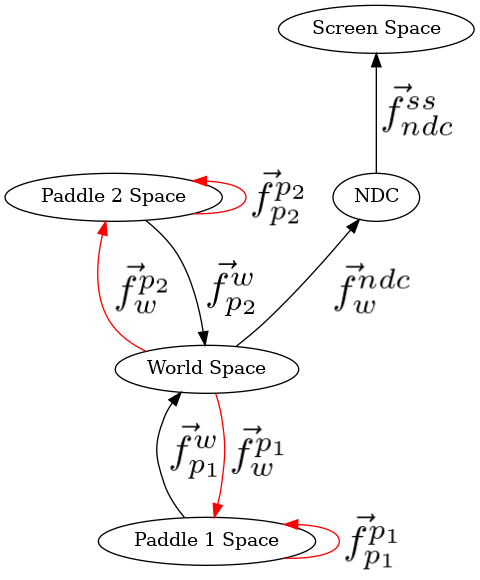
The images of the transformation sequence below should show how brain-dead it is, and the Cayley graph is gross.

But from this we will learn something important.

translating back to the origin

resetting the coordinate system

rotating

resetting the coordinate system

and them translating them back to the paddle space origin

Cayley Graph¶

Note, this is gross, and the edge from the paddlespace to itself doesn’t even make any sense, but the author did not know how else to represent this code.