Relative Objects - Demo 11

Purpose

Introduce relative objects, by making a small blue square that is defined relative to the left paddle, but offset some in the x direction. When the paddle on the left moves or rotates, the blue square moves with it, because it is defined relative to it.

Demo 11

Demo 11

How to Execute

Load src/demo11/demo.py in Spyder and hit the play button

Move the Paddles using the Keyboard

Keyboard Input

Action

w

Move Left Paddle Up

s

Move Left Paddle Down

k

Move Right Paddle Down

i

Move Right Paddle Up

d

Increase Left Paddle’s Rotation

a

Decrease Left Paddle’s Rotation

l

Increase Right Paddle’s Rotation

j

Decrease Right Paddle’s Rotation

UP

Move the camera up, moving the objects down

DOWN

Move the camera down, moving the objects up

LEFT

Move the camera left, moving the objects right

RIGHT

Move the camera right, moving the objects left

Description

Cayley Graph

In the graph below, all we have added is “Square space”, relative to paddle 1 space.

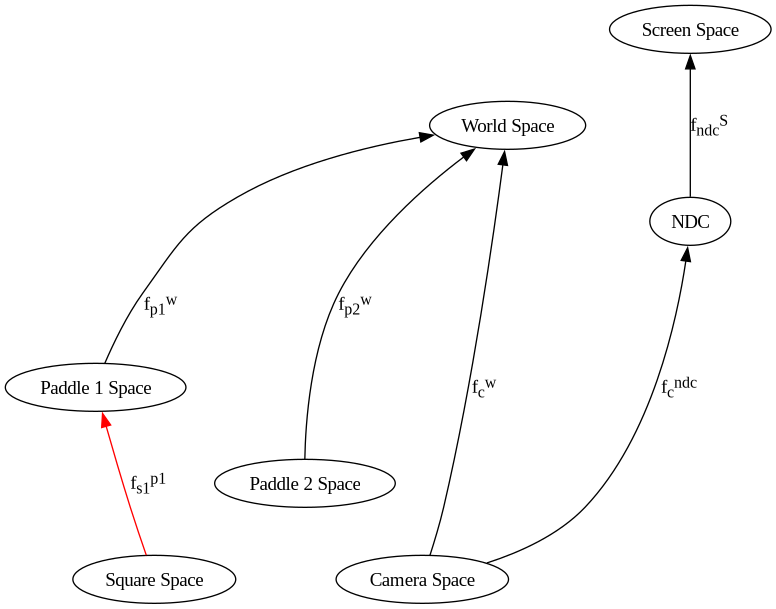
Demo 11

Demo 11

In the picture below, in 3D space, we see that the square has its own modelspace (as evidenced by the 3 arrows), and we are going to define its position and orientation relative to paddle 1.

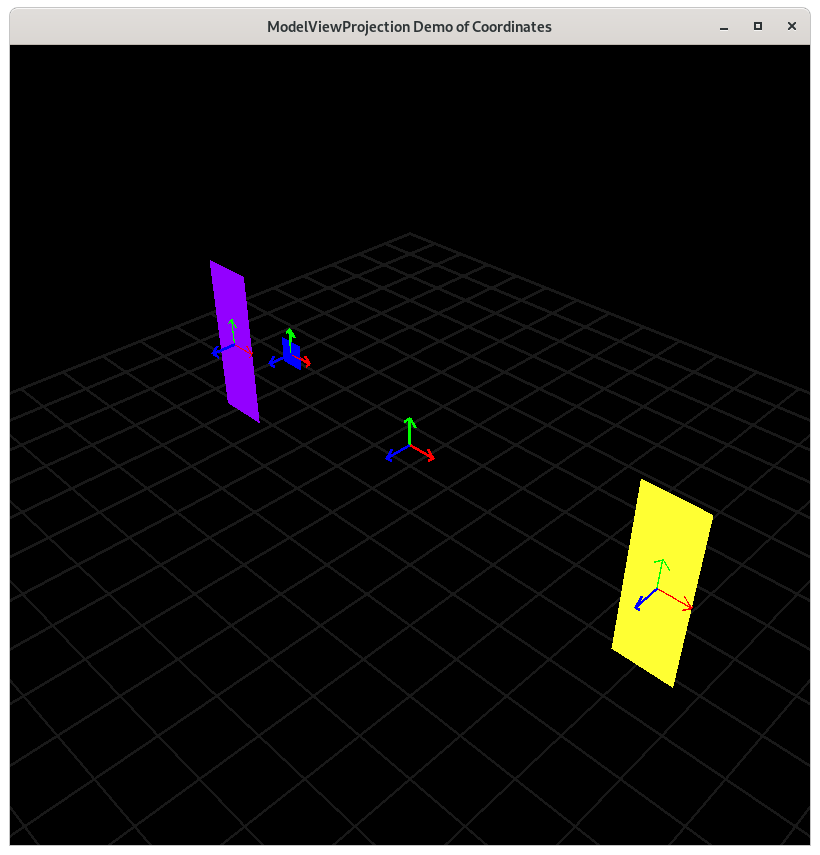
Coordinate Frames

Coordinate Frames

Code

Define the geometry of the square in its own modelspace.

src/demo11/demo.py
187square: list[Vertex] = [
188    Vertex(x=-0.5, y=-0.5),
189    Vertex(x=0.5, y=-0.5),
190    Vertex(x=0.5, y=0.5),
191    Vertex(x=-0.5, y=0.5),
192]

Event Loop

src/demo11/demo.py
235while not glfw.window_should_close(window):

...

Draw paddle 1, just as before.

src/demo11/demo.py
255    glColor3f(paddle1.r, paddle1.g, paddle1.b)
256
257    glBegin(GL_QUADS)
258    for paddle1_vertex_ms in paddle1.vertices:
259        paddle1_vertex_ws: Vertex = paddle1_vertex_ms.rotate(
260            paddle1.rotation
261        ).translate(paddle1.position)
262        paddle1_vertex_cs: Vertex = paddle1_vertex_ws.translate(-camera.position_ws)
263        paddle1_vertex_ndc: Vertex = paddle1_vertex_cs.uniform_scale(scalar=1.0 / 10.0)
264        glVertex2f(paddle1_vertex_ndc.x, paddle1_vertex_ndc.y)
265    glEnd()

As a refresher, the author recommends reading the code from modelspace to worldspace from the bottom up, and from worldspace to NDC from top down.

  • Read from modelspace to world space, bottom up

  • Reset the coordinate system

  • Read from world space to camera space, knowing that camera transformations are implemented as the inverse of placing the camera space in world space.

  • Reset the coordinate system

  • Read camera-space to NDC

New part! Draw the square relative to the first paddle! Translate the square to the right by 2 units. We are dealing with a -1 to 1 world space, which later gets scaled down to NDC.

src/demo11/demo.py
269    glColor3f(0.0, 0.0, 1.0)
270    glBegin(GL_QUADS)
271    for model_space in square:
272        paddle1space: Vertex = model_space.translate(Vertex(x=2.0, y=0.0))
273        world_space: Vertex = paddle1space.rotate(paddle1.rotation).translate(
274            paddle1.position
275        )
276        camera_space: Vertex = world_space.translate(-camera.position_ws)
277        ndc: Vertex = camera_space.uniform_scale(scalar=1.0 / 10.0)
278        glVertex2f(ndc.x, ndc.y)
279    glEnd()

Towards that, we need to do all of the transformations to the square that we would to the paddle, and then do any extra transformations afterwards.

As such, read

  • Read paddle1space to world space, from bottom up

If we were to plot the square now, it would be in paddle 1’s space. We don’t want that, we want in to be moved in the X direction some units. Therefore

  • Read modelspace to paddle1space, from bottom up

  • Reset the coordinate system.

Now the square’s geometry will be in its own space!

  • Read from worldspace to camera-space, knowing that camera transformations are implemented as the inverse of placing the camera space in world space.

  • Reset the coordinate system

  • Read camera-space to NDC

Draw paddle 2 just like before.

src/demo11/demo.py
283    glColor3f(paddle2.r, paddle2.g, paddle2.b)
284
285    glBegin(GL_QUADS)
286    for paddle2_vertex_ms in paddle2.vertices:
287        paddle2_vertex_ws: Vertex = paddle2_vertex_ms.rotate(
288            paddle2.rotation
289        ).translate(paddle2.position)
290        paddle2_vertex_cs: Vertex = paddle2_vertex_ws.translate(-camera.position_ws)
291        paddle2_vertex_ndc: Vertex = paddle2_vertex_cs.uniform_scale(1.0 / 10.0)
292        glVertex2f(paddle2_vertex_ndc.x, paddle2_vertex_ndc.y)
293    glEnd()