Matrix Stacks - Demo 19¶
Objective¶
Replace lambda stacks with OpenGL 2.1 matrix stacks, provided by the driver for your graphics card. This is how preshader opengl worked.
The function stack allowed us to aggregate the entirety of the transformations from modelspace to NDC, by creating a context of transformations, and a function to do the conversion. We then needed to push or pop functions from the stack, depending on what space transition we were currently dealing with.
A given matrix in OpenGL2.1 is the equivalent of a function stack; given one matrix, it can perform a sequence of transformations from one space to another, with one matrix multiplication.
OpenGL 2.1 deals with two different types of matrices: 1) the projection matrix, which effectively is the function from camera space to NDC (clip space) and 2) The model-view matrix, which deals with the transformations from modelspace to camera space.
Given that a matrix can perform a sequence of transformations across multiple spaces in the Cayley graph, it may appear that we no longer need any notion of a stack, as we had in the function stacks. But that is not true. For the Model-View matrix, we still need a stack of matrices, so that we can return to a previous transformation sequence. For instance, if we are at world space, the Model-View matrix at the top of the matrix stack will convert from world space to camera space. But we need to draw two relative child spaces to world space, paddle 1 space and paddle 2 space. So before we do the transformations to paddle 1 space, we “push” a copy of the current model-view matrix to the top of the model-view matrix stack, so that after we draw paddle 1 and the square, we can “pop” that matrix off, leaving us the matrix at the top of the model-view matrix stack that represents world space, so that we can then begin to transform to paddle 2 space.
The concepts behind the function stack, in which the first function added to the stack is the last function applied, hold true for matrices as well. But matrices are a much more efficient representation computationally than the function stack, and instead of adding fns and later having to remove them, we can save onto the current frame of reference with a “glPushStack”, and restore the saved state by “glPopStack”.
Use glPushMatrix and glPopMatrix to save/restore a local coordinate system, that way a tree of objects can be drawn without one child destroying the relative coordinate system of the parent node.
In mvpVisualization/pushmatrix/pushmatrix.py, the grayed out coordinate system is one that has been pushed onto the stack, and it regains its color when it is reactivated by “glPopMatrix”
How to Execute¶
Load src/modelviewprojection/demo19.py in Spyder and hit the play button.
Move the Paddles using the Keyboard¶
Keyboard Input |
Action |
|---|---|
w |
Move Left Paddle Up |
s |
Move Left Paddle Down |
k |
Move Right Paddle Down |
i |
Move Right Paddle Up |
d |
Increase Left Paddle’s Rotation |
a |
Decrease Left Paddle’s Rotation |
l |
Increase Right Paddle’s Rotation |
j |
Decrease Right Paddle’s Rotation |
UP |
Move the camera up, moving the objects down |
DOWN |
Move the camera down, moving the objects up |
LEFT |
Move the camera left, moving the objects right |
RIGHT |
Move the camera right, moving the objects left |
q |
Rotate the square around its center |
e |
Rotate the square around paddle 1’s center |
Description¶
First thing to note is that we are now using OpenGL 2.1’s official transformation procedures, and in the projection transformation, they flip the z axis, making it a left hand coordinate system. The reason for this is long, and I have begun discusses in the “Standard Perspective Matrix” section, but it is an incomplete section for now. But for now, all it means that we have to change how the depth test will be configured, as after the projection transformation, the far z value is 1.0, and the near z value is -1
The clear depth that is set for each fragment each frame is now 1.0, and the test for a given fragment to overwrite the color in the color buffer is changed to be less than or equal to.
Code¶
54GL.glEnable(GL.GL_DEPTH_TEST)
55GL.glClearDepth(1.0)
56GL.glDepthFunc(GL.GL_LEQUAL)
The Event Loop¶
Set the model, view, and projection matrix to the identity matrix. This just means that the functions (currently) will not transform data. In univariate terms, f(x) = x
227 GL.glMatrixMode(GL.GL_PROJECTION)
228 GL.glLoadIdentity()
229 GL.glMatrixMode(GL.GL_MODELVIEW)
230 GL.glLoadIdentity()
change the projection matrix to convert the frustum to clip space set the projection matrix to be perspective. Since the viewport is always square, set the aspect ratio to be 1.0. We are now going to clip space instead of to NDC, which we be discussed in the next chapter.
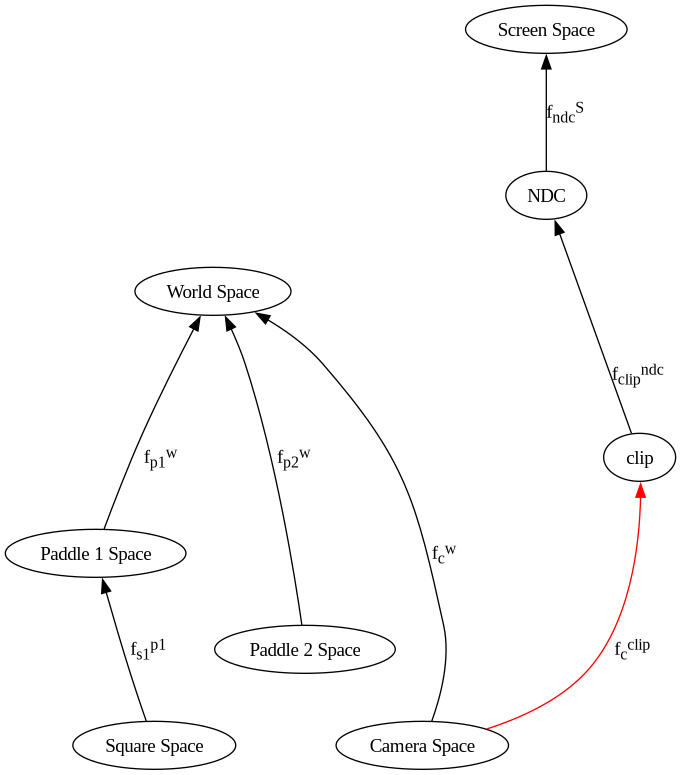
Turn our NDC into Clip Space¶
235 GL.glMatrixMode(GL.GL_PROJECTION)
236 GLU.gluPerspective(
237 45.0, # field_of_view
238 1.0, # aspect_ration
239 0.1, # near_z
240 1000.0, # far_z
241 )
“glMatrixMode” tells the computer which matrix stack should be the active one, against which subsequent matrix operations which affect. In this case, we set the current matrix stack to be the projection one. We then call “gluPerspective” to set the projection transformation, which we covered in previous sections, and we will ignore the implementation of it; it is now a black box.
Now onto camera space!
The camera’s position could be described relative to world space by the following sequence of transformations.
# glTranslate(camera.x, camera.y, camera.z)
# glRotatef(math.degrees(camera.rot_y), 0.0, 1.0, 0.0)
# glRotatef(math.degrees(camera.rot_x), 1.0, 0.0, 0.0)
Therefore, to take the object’s world space coordinates and transform them into camera space, we need to do the inverse operations to the view stack.
246 GL.glMatrixMode(GL.GL_MODELVIEW)
247
248 GL.glRotatef(math.degrees(-camera.rot_x), 1.0, 0.0, 0.0)
249 GL.glRotatef(math.degrees(-camera.rot_y), 0.0, 1.0, 0.0)
250 GL.glTranslate(-camera.x, -camera.y, -camera.z)
First thing we did was set the current matrix to be the model-view matrix, instead of the projection matrix. Most of our work will be with the model-view matrix, as looking at the Cayley graph, there’s only one function from camera space to NDC. N.B., OpenGL 2.1 transformations use degrees, not radians, so we need to convert to degrees.
Unlike in the lambda stack demo, in which a new function was added to the top of the stack, without modifying any functions below it on the stack, with OpenGL matrices, each transformation, such as translate, rotate, and scale, actually destructively modifies the matrix at the top of the stack, as matrices can be premultiplied together for efficiency.
In linear algebra terms, the matrix multiplication takes place, but then the resulting values of the matrix replace the values of the matrix at the top of the stack.
|a b| |e f| |ae+bg af+bh|
|c d| * |g h| = |ce+dg cf+dh|
This means that rotate_x, rotate_y, translate, etc are destructive operations to the matrix on the top of the stack. Instead of creating new matrix to the top of the stack of matrices, these operations aggregate the transformations, but add no new matrices to the stack, and as such are destructive operations to the current matrix.
But many times we need to hold onto a transformation stack (matrix), so that we can do something else now, and return to this context later, so we have a stack composed of matrices.
This is what glPushMatrix, and glPopMatrix do.
“PushMatrix” describes what the function does, but its purpose is to save onto the current coordinate system for later drawing modelspace data.
The model-view matrix stack is currently the transformation from world space into camera space. Since we now have to draw paddle 1, the square, and paddle 2, save onto the current model-view stack, to hold onto world space, so that after we draw paddle 1 and the square, we can restore the world space, so that paddle 2 can be drawn relative to it.
263 GL.glPushMatrix()
draw paddle 1¶
Unlike in previous demos before the lambda stack, because the transformations are now on a stack, the functions on the model stack can be read forwards, where each operation translates/rotates/scales the current space.
glVertex data is specified in modelspace coordinates, but since we loaded the projection matrix and the modelview matrix into OpenGL, glVertex3f will apply those transformations for us [1]!
267 GL.glColor3f(*iter(paddle1.color))
268
269 GL.glTranslate(
270 paddle1.position[0],
271 paddle1.position[1],
272 0.0,
273 )
274 GL.glRotatef(math.degrees(paddle1.rotation), 0.0, 0.0, 1.0)
275
276 GL.glBegin(GL.GL_QUADS)
277 for p1_v_ms in paddle1.vertices:
278 GL.glVertex3f(
279 p1_v_ms[0],
280 p1_v_ms[1],
281 p1_v_ms[2],
282 )
283 GL.glEnd()
draw the square relative to paddle 1¶
Since the modelstack is already in paddle1’s space just add the transformations relative to it before paddle 2 is drawn, we need to remove the square’s 3 modelspace transformations
289 # draw the square
290 # given that no nodes are defined relative to the square, we do not need
291 # to push a matrix. Here we will do so anyway, just to clarify what is
292 # happening
293 GL.glPushMatrix()
294 # the current model matrix will be copied and then the copy will be
295 # pushed onto the model stack
296 GL.glColor3f(0.0, 0.0, 1.0)
297
298 # these functions change the current model matrix
299 GL.glTranslate(0.0, 0.0, -1.0)
300 GL.glRotatef(math.degrees(rotation_around_paddle1), 0.0, 0.0, 1.0)
301 GL.glTranslate(2.0, 0.0, 0.0)
302 GL.glRotatef(math.degrees(square_rotation), 0.0, 0.0, 1.0)
303
304 GL.glBegin(GL.GL_QUADS)
305 for ms in square_vertices:
306 GL.glVertex3f(ms[0], ms[1], ms[2])
307 GL.glEnd()
308 GL.glPopMatrix()
309 # the mode matrix that was on the model stack before the square
310 # was drawn will be restored
311 GL.glPopMatrix()
draw paddle 2¶
No need to push matrix here, as this is the last object that we are drawing, and upon the next iteration of the event loop, all 3 matrices will be reset to the identity
315 # draw paddle 2. Nothing is defined relative to paddle to, so we don't
316 # need to push matrix, and on the next iteration of the event loop,
317 # all matrices will be cleared to identity, so who cares if we
318 # mutate the values for now.
319 GL.glColor3f(*iter(paddle2.color))
320
321 GL.glTranslate(
322 paddle2.position[0],
323 paddle2.position[1],
324 0.0,
325 )
326 GL.glRotatef(math.degrees(paddle2.rotation), 0.0, 0.0, 1.0)
327
328 GL.glBegin(GL.GL_QUADS)
329 for p2_v_ms in paddle2.vertices:
330 GL.glVertex3f(
331 p2_v_ms[0],
332 p2_v_ms[1],
333 p2_v_ms[2],
334 )
335 GL.glEnd()