Add Translate Method to Vector - Demo 05

Objective

Restructure the code towards the model view projection pipeline.

Transforming vertices, such as translating, is one of the core concept of computer graphics.

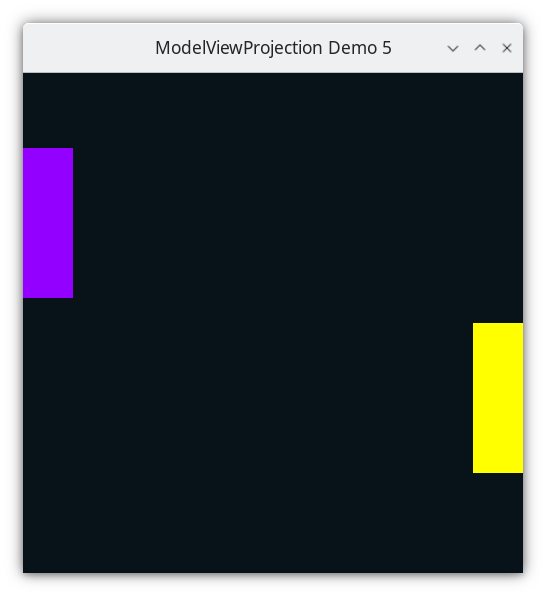
Demo 05

Demo 05

How to Execute

Load src/modelviewprojection/demo05.py in Spyder and hit the play button.

Move the Paddles using the Keyboard

Keyboard Input

Action

w

Move Left Paddle Up

s

Move Left Paddle Down

k

Move Right Paddle Down

i

Move Right Paddle Up

Translation

Dealing with the two Paddles the way we did before is not ideal. Both Paddles have the same size, although they are placed in different spots of the screen. We should be able to a set of vertices for the Paddle, relative to the paddle’s center, that is independent of its placement in NDC.

Rather than using values for each vector relative to NDC, in the Paddle data structure, each vector will be an offset from the center of the Paddle. The center of the paddle will be considered x=0, y=0. Before rendering, each Paddle’s vertices will need to be translated to its center relative to NDC.

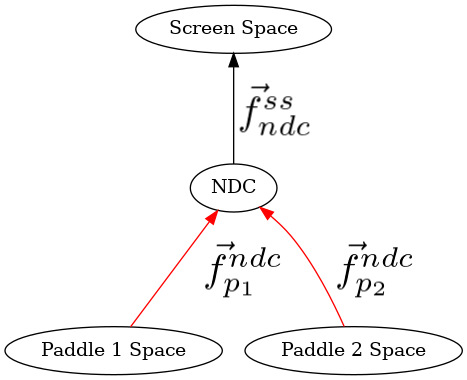
Paddle space

All methods on vertices will be returning new vertices, rather than mutating the instance variables. The author does this on purpose to enable method-chaining the Python methods, which will be useful later on.

Method-chaining is the equivalent of function composition in math.

Code

Data Structures

src/modelviewprojection/demo05.py
62@dataclasses.dataclass
63class Vector2D(mu1d.Vector1D):
64    y: float  #: The y-component of the 2D Vector

We added a translate method to the Vector class. Given a translation amount, the vector will be shifted by that amount. This is a primitive that we will be using to transform from one space to another.

If the reader wishes to use the data structures to test them out, import them and try the methods

>>> from modelviewprojection.mathutils2d import Vector
>>> a = demo.Vector(x=1,y=2)
>>> a.translate(demo.Vector(x=3,y=4))
Vector(x=4, y=6)

Note the use of “keyword arguments”. Without using keyword arguments, the code might look like this:

>>> from modelviewprojection.mathutils2d import Vector
>>> a = demo.Vector(1,2)
>>> a.translate(demo.Vector(x=3,y=4))
Vector(x=4, y=6)

Keyword arguments allow the reader to understand the purpose of the parameters are, at the call-site of the function.

src/modelviewprojection/demo05.py
87@dataclasses.dataclass
88class Paddle:
89    vertices: list[mu2d.Vector2D]
90    color: colorutils.Color3
91    position: mu2d.Vector2D

Add a position instance variable to the Paddle class. This position is the center of the paddle, defined relative to NDC. The vertices of the paddle will be defined relative to the center of the paddle.

Instantiation of the Paddles

src/modelviewprojection/demo05.py
 96paddle1: Paddle = Paddle(
 97    vertices=[
 98        mu2d.Vector2D(x=-0.1, y=-0.3),
 99        mu2d.Vector2D(x=0.1, y=-0.3),
100        mu2d.Vector2D(x=0.1, y=0.3),
101        mu2d.Vector2D(x=-0.1, y=0.3),
102    ],
103    color=colorutils.Color3(r=0.578123, g=0.0, b=1.0),
104    position=mu2d.Vector2D(-0.9, 0.0),
105)
106
107paddle2: Paddle = Paddle(
108    vertices=[
109        mu2d.Vector2D(-0.1, -0.3),
110        mu2d.Vector2D(0.1, -0.3),
111        mu2d.Vector2D(0.1, 0.3),
112        mu2d.Vector2D(-0.1, 0.3),
113    ],
114    color=colorutils.Color3(r=1.0, g=1.0, b=0.0),
115    position=mu2d.Vector2D(0.9, 0.0),
116)

  • The vertices are now defined as relative distances from the center of the paddle. The centers of each paddle are placed in positions relative to NDC that preserve the positions of the paddles, as they were in the previous demo.

Handling User Input

src/modelviewprojection/demo05.py
121def handle_movement_of_paddles() -> None:
122    global paddle1, paddle2
123
124    if glfw.get_key(window, glfw.KEY_S) == glfw.PRESS:
125        paddle1.position.y -= 0.1
126    if glfw.get_key(window, glfw.KEY_W) == glfw.PRESS:
127        paddle1.position.y += 0.1
128    if glfw.get_key(window, glfw.KEY_K) == glfw.PRESS:
129        paddle2.position.y -= 0.1
130    if glfw.get_key(window, glfw.KEY_I) == glfw.PRESS:
131        paddle2.position.y += 0.1

  • We put the transformation on the center of the paddle, instead of directly on each vector. This is because the vertices are defined relative to the center of the paddle.

The Event Loop

src/modelviewprojection/demo05.py
140while not glfw.window_should_close(window):
141    while (
142        glfw.get_time()
143        < time_at_beginning_of_previous_frame + 1.0 / TARGET_FRAMERATE
144    ):
145        pass
146
147    time_at_beginning_of_previous_frame = glfw.get_time()
148
149    glfw.poll_events()
150
151    width, height = glfw.get_framebuffer_size(window)
152    GL.glViewport(0, 0, width, height)
153    GL.glClear(sum([GL.GL_COLOR_BUFFER_BIT, GL.GL_DEPTH_BUFFER_BIT]))
154
155    draw_in_square_viewport()
156    handle_movement_of_paddles()
src/modelviewprojection/demo05.py
160    GL.glColor3f(*iter(paddle1.color))
161
162    GL.glBegin(GL.GL_QUADS)
163    for p1_v_ms in paddle1.vertices:
164        paddle1_vector_ndc: mu.Vector = T(paddle1.position)(p1_v_ms)
165        # we could have written
166        # paddle1_vector_ndc: mu.Vector = paddle1.position + p1_v_ms
167        GL.glVertex2f(paddle1_vector_ndc.x, paddle1_vector_ndc.y)
168    GL.glEnd()

Here each of paddle 1’s vertices, which are in their Modelspace, are converted to NDC by calling the translate method on the vector. This function corresponds to the Cayley graph below, the function from Paddle 1 space to NDC.

src/modelviewprojection/demo05.py
172    GL.glColor3f(*iter(paddle2.color))
173
174    p2_fn: mu2d.InvertibleFunction = T(paddle2.position)
175    GL.glBegin(GL.GL_QUADS)
176    for p2_v_ms in paddle2.vertices:
177        paddle2_vector_ndc: mu.Vector = p2_fn(p2_v_ms)
178        GL.glVertex2f(paddle2_vector_ndc.x, paddle2_vector_ndc.y)
179    GL.glEnd()

Paddle space

The only part of the diagram that we need to think about right now is the function that converts from paddle1’s space to NDC, and from paddle2’s space to NDC.

These functions in the Python code are the translation of the paddle’s center (i.e. paddle1.position) by the vector’s offset from the center.

N.B. In the code, I name the vertices by their space. I.e. “modelSpace” instead of “vector_relative_to_modelspace”. I do this to emphasize that you should view the transformation as happening to the “graph paper”, instead of to each of the points. This will be explained more clearly later.