Lambda Stack - Demo 16¶
Objective¶
Remove repetition in the coordinate transformations, as previous demos had very similar transformations, especially from camera space to NDC space. Each edge of the graph of objects should only be specified once per frame.
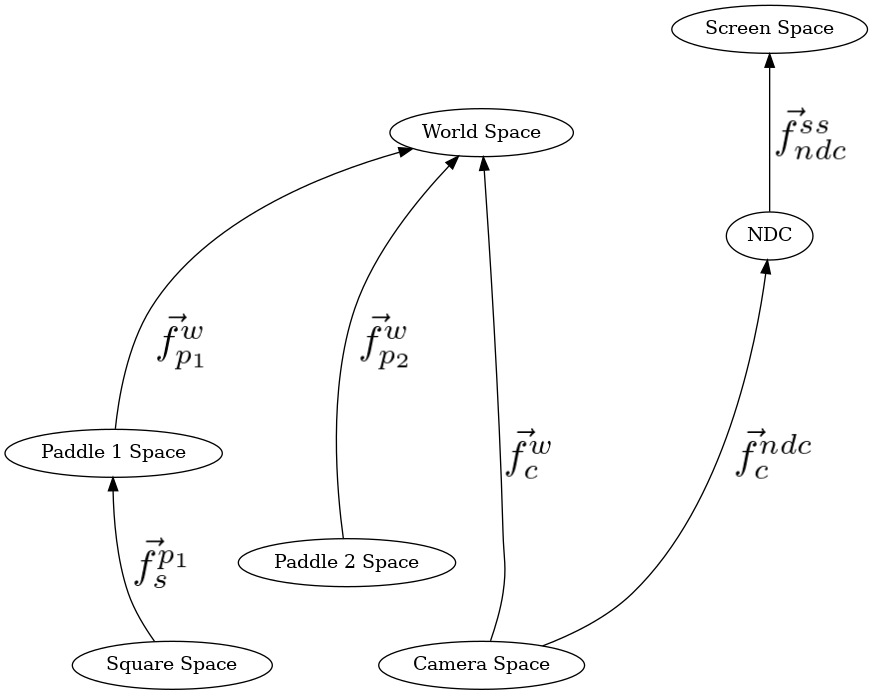
Full Cayley graph.¶
Noticing in the previous demos that the lower parts of the transformations have a common pattern, we can create a stack of functions for later application. Before drawing geometry, we add any functions to the top of the stack, apply all of our functions in the stack to our modelspace data to get NDC data, and before we return to the parent node, we pop the functions we added off of the stack, to ensure that we return the stack to the state that the parent node gave us.
To explain in more detail —
What’s the difference between drawing paddle 1 and the square?
Here is paddle 1 code
208 GL.glColor3f(*iter(paddle1.color))
209 GL.glBegin(GL.GL_QUADS)
210 for p1_v_ms in paddle1.vertices:
211 ms_to_ndc: mu3d.InvertibleFunction = mu3d.compose(
212 [
213 # camera space to NDC
214 mu3d.uniform_scale(1.0 / 10.0),
215 # world space to camera space
216 mu3d.inverse(mu3d.translate(camera.position_ws)),
217 # model space to world space
218 mu3d.compose(
219 [
220 mu3d.translate(paddle1.position),
221 mu3d.rotate_z(paddle1.rotation),
222 ]
223 ),
224 ]
225 )
226
227 paddle1_vector_ndc: mu3d.Vector3D = ms_to_ndc(p1_v_ms)
228 GL.glVertex3f(
229 paddle1_vector_ndc.x, paddle1_vector_ndc.y, paddle1_vector_ndc.z
230 )
231 GL.glEnd()
Here is the square’s code:
235 # draw square
236 GL.glColor3f(0.0, 0.0, 1.0)
237 GL.glBegin(GL.GL_QUADS)
238 for ms in square:
239 ms_to_ndc: mu3d.InvertibleFunction = mu3d.compose(
240 [
241 # camera space to NDC
242 mu3d.uniform_scale(1.0 / 10.0),
243 # world space to camera space
244 mu3d.inverse(mu3d.translate(camera.position_ws)),
245 # model space to world space
246 mu3d.compose(
247 [
248 mu3d.translate(paddle1.position),
249 mu3d.rotate_z(paddle1.rotation),
250 ]
251 ),
252 # square space to paddle 1 space
253 mu3d.compose(
254 [
255 mu3d.translate(mu3d.Vector3D(x=0.0, y=0.0, z=-1.0)),
256 mu3d.rotate_z(rotation_around_paddle1),
257 mu3d.translate(mu3d.Vector3D(x=2.0, y=0.0, z=0.0)),
258 mu3d.rotate_z(square_rotation),
259 ]
260 ),
261 ]
262 )
263 square_vector_ndc: mu3d.Vector3D = ms_to_ndc(ms)
264 GL.glVertex3f(
265 square_vector_ndc.x, square_vector_ndc.y, square_vector_ndc.z
266 )
267 GL.glEnd()
The only difference is the square’s modelspace to paddle1 space. Everything else is exactly the same. In a graphics program, because the scene is a hierarchy of relative objects, it is unwise to put this much repetition in the transformation sequence. Especially if we might change how the camera operates, or from perspective to ortho. It would required a lot of code changes. And I don’t like reading from the bottom of the code up. Code doesn’t execute that way. I want to read from top to bottom.
When reading the transformation sequences in the previous demos from top down the transformation at the top is applied first, the transformation at the bottom is applied last, with the intermediate results method-chained together. (look up above for a reminder)
With a function stack, the function at the top of the stack (f5) is applied first, the result of this is then given as input to f4 (second on the stack), all the way down to f1, which was the first fn to be placed on the stack, and as such, the last to be applied. (Last In First Applied - LIFA)
|-------------------|
(MODELSPACE) | |
(x,y,z)-> | f5 |--
|-------------------| |
|
-------------------------
|
| |-------------------|
| | |
->| f4 |--
|-------------------| |
|
-------------------------
|
| |-------------------|
| | |
->| f3 |--
|-------------------| |
|
-------------------------
|
| |-------------------|
| | |
->| f2 |--
|-------------------| |
|
-------------------------
|
| |-------------------|
| | |
->| f1 |--> (x,y,z) NDC
|-------------------|
So, in order to ensure that the functions in a stack will execute in the same order as all of the previous demos, they need to be pushed onto the stack in reverse order.
This means that from modelspace to world space, we can now read the transformations FROM TOP TO BOTTOM!!!! SUCCESS!
Then, to draw the square relative to paddle one, those six transformations will already be on the stack, therefore only push the differences, and then apply the stack to the paddle’s modelspace data.
How to Execute¶
Load src/modelviewprojection/demo16.py in Spyder and hit the play button.
Move the Paddles using the Keyboard¶
Keyboard Input |
Action |
|---|---|
w |
Move Left Paddle Up |
s |
Move Left Paddle Down |
k |
Move Right Paddle Down |
i |
Move Right Paddle Up |
d |
Increase Left Paddle’s Rotation |
a |
Decrease Left Paddle’s Rotation |
l |
Increase Right Paddle’s Rotation |
j |
Decrease Right Paddle’s Rotation |
UP |
Move the camera up, moving the objects down |
DOWN |
Move the camera down, moving the objects up |
LEFT |
Move the camera left, moving the objects right |
RIGHT |
Move the camera right, moving the objects left |
q |
Rotate the square around its center |
e |
Rotate the square around paddle 1’s center |
Description¶
Function stack. Internally it has a list, where index 0 is the bottom of the stack. In python we can store any object as a variable, and we will be storing functions which transform a vector to another vector, through the “modelspace_to_ndc” method.
890@dataclasses.dataclass
891class FunctionStack:
892 stack: list[InvertibleFunction] = dataclasses.field(
893 default_factory=lambda: []
894 )
895
896 def push(self, o: InvertibleFunction):
897 self.stack.append(o)
898
899 def pop(self) -> InvertibleFunction:
900 return self.stack.pop()
901
902 def clear(self):
903 self.stack.clear()
904
905 def modelspace_to_ndc_fn(self) -> InvertibleFunction:
906 return compose(self.stack)
907
908
909fn_stack = FunctionStack()
Define four functions, which we will compose on the stack.
Push identity onto the stack, which will will never pop off of the stack.
580def test_vec3_fn_stack():
581 identity: InvertibleFunction = mu.uniform_scale(1)
582
583 mu.fn_stack.push(identity)
584 assert mu.Vector1D(1) == mu.fn_stack.modelspace_to_ndc_fn()(mu.Vector1D(1))
585
586 add_one: InvertibleFunction = mu.translate(mu.Vector1D(1))
587
588 mu.fn_stack.push(add_one)
589 assert mu.Vector1D(2) == mu.fn_stack.modelspace_to_ndc_fn()(
590 mu.Vector1D(1)
591 ) # x + 1 = 2
592
593 multiply_by_2: InvertibleFunction = mu.uniform_scale(2)
594
595 mu.fn_stack.push(multiply_by_2) # (x * 2) + 1 = 3
596 assert mu.Vector1D(3) == mu.fn_stack.modelspace_to_ndc_fn()(mu.Vector1D(1))
597
598 add_5: InvertibleFunction = mu.translate(mu.Vector1D(5))
599
600 mu.fn_stack.push(add_5) # ((x + 5) * 2) + 1 = 13
601 assert mu.Vector1D(13) == mu.fn_stack.modelspace_to_ndc_fn()(mu.Vector1D(1))
602
603 mu.fn_stack.pop()
604 assert mu.Vector1D(3) == mu.fn_stack.modelspace_to_ndc_fn()(
605 mu.Vector1D(1)
606 ) # (x * 2) + 1 = 3
607
608 mu.fn_stack.pop()
609 assert mu.Vector1D(2) == mu.fn_stack.modelspace_to_ndc_fn()(
610 mu.Vector1D(1)
611 ) # x + 1 = 2
612
613 mu.fn_stack.pop()
614 assert mu.Vector1D(1) == mu.fn_stack.modelspace_to_ndc_fn()(
615 mu.Vector1D(1)
616 ) # x = 1
Event Loop¶
188while not glfw.window_should_close(window):
...
In previous demos, camera_space_to_ndc_space_fn was always the last function called in the method chained pipeline. Put it on the bottom of the stack, by pushing it first, so that “modelspace_to_ndc” calls this function last. Each subsequent push will add a new function to the top of the stack.
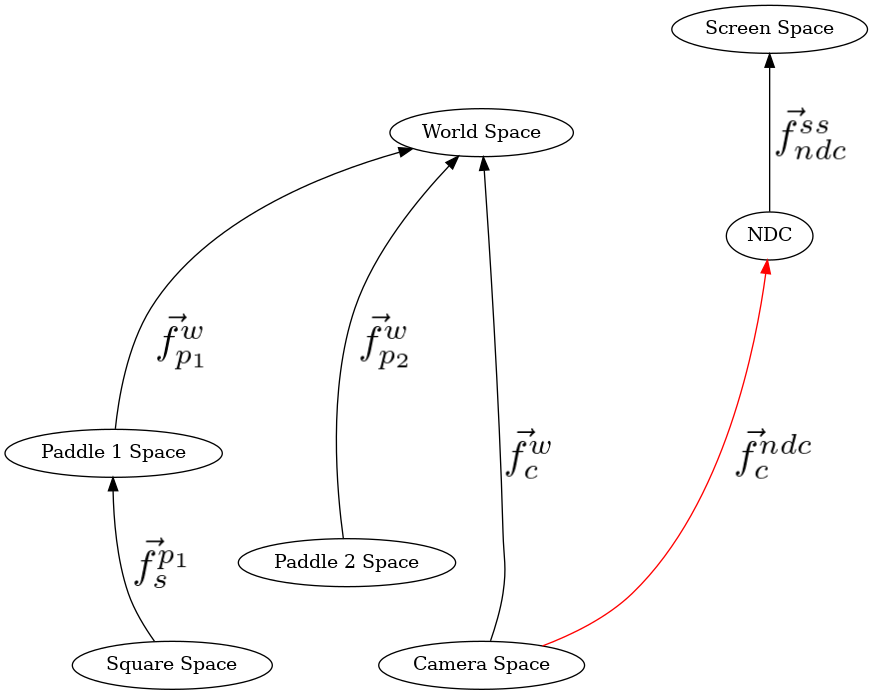
208 # camera space to NDC
209 mu3d.fn_stack.push(mu3d.uniform_scale(1.0 / 10.0))
Unlike in previous demos in which we read the transformations from modelspace to world space backwards; this time because the transformations are on a stack, the fns on the model stack can be read forwards, where each operation translates/rotates/scales the current space
The camera’s position and orientation are defined relative to world space like so, read top to bottom:
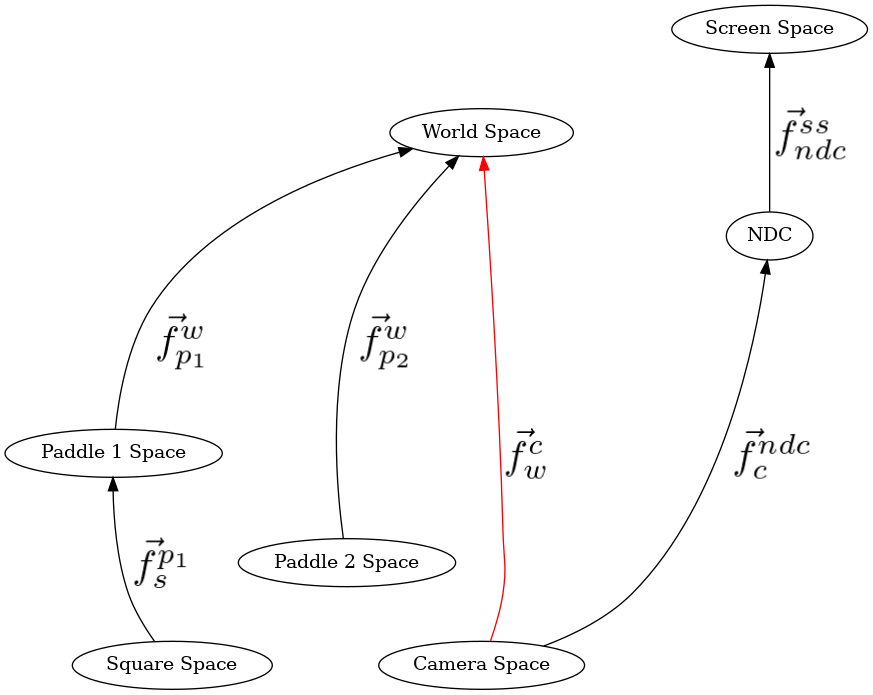
But, since we need to transform world-space to camera space, they must be inverted by reversing the order, and negating the arguments
Therefore the transformations to put the world space into camera space are.
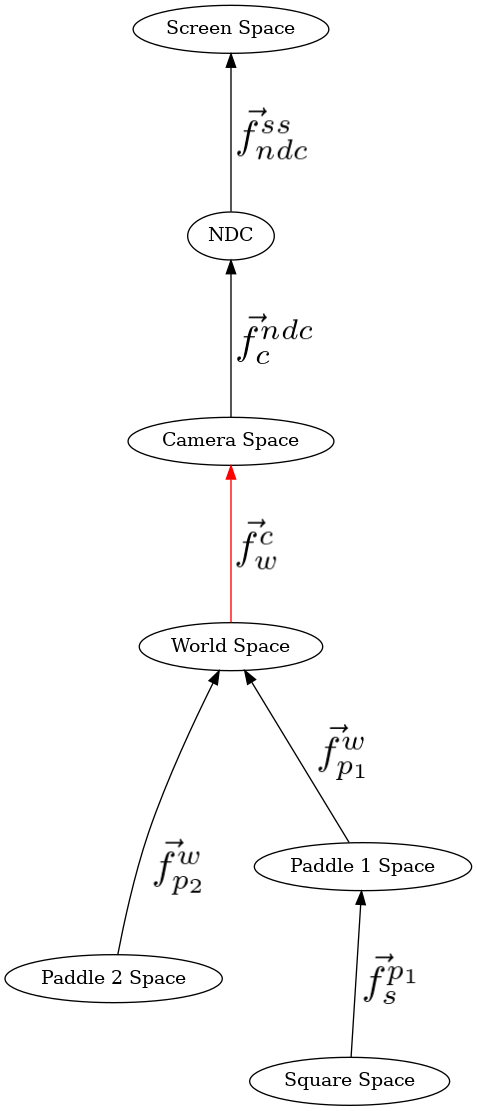
213 # world space to camera space
214 mu3d.fn_stack.push(mu3d.inverse(mu3d.translate(camera.position_ws)))
draw paddle 1¶
Unlike in previous demos in which we read the transformations from modelspace to world space backwards; because the transformations are on a stack, the fns on the model stack can be read forwards, where each operation translates/rotates/scales the current space
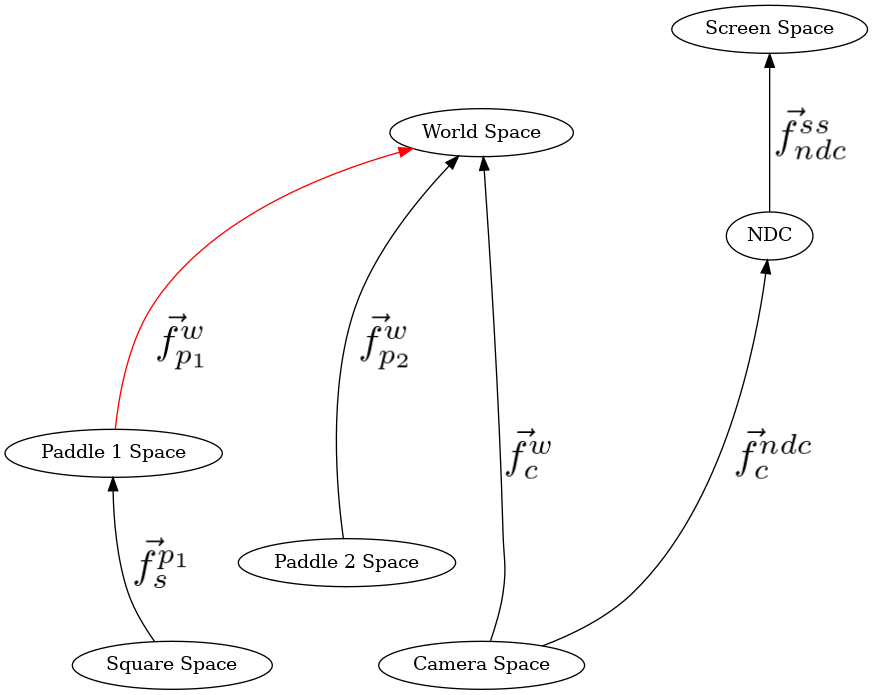
218 # paddle 1 model space to world space
219 mu3d.fn_stack.push(
220 mu3d.compose(
221 [mu3d.translate(paddle1.position), mu3d.rotate_z(paddle1.rotation)]
222 )
223 )
for each of the modelspace coordinates, apply all of the procedures on the stack from top to bottom this results in coordinate data in NDC space, which we can pass to glVertex3f
227 GL.glColor3f(*iter(paddle1.color))
228 GL.glBegin(GL.GL_QUADS)
229 for p1_v_ms in paddle1.vertices:
230 paddle1_vector_ndc = mu3d.fn_stack.modelspace_to_ndc_fn()(p1_v_ms)
231 GL.glVertex3f(
232 paddle1_vector_ndc.x,
233 paddle1_vector_ndc.y,
234 paddle1_vector_ndc.z,
235 )
236 GL.glEnd()
draw the square¶
since the modelstack is already in paddle1’s space, and since the blue square is defined relative to paddle1, just add the transformations relative to it before the blue square is drawn. Draw the square, and then remove these 4 transformations from the stack (done below)
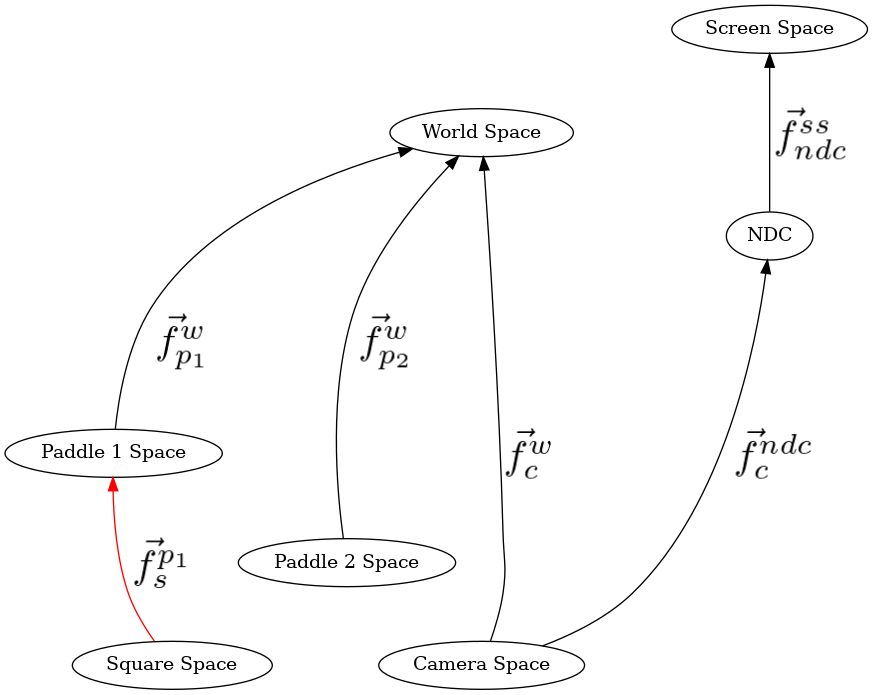
240 mu3d.fn_stack.push(
241 mu3d.compose(
242 [
243 mu3d.translate(mu3d.Vector3D(x=0.0, y=0.0, z=-1.0)),
244 mu3d.rotate_z(rotation_around_paddle1),
245 mu3d.translate(mu3d.Vector3D(x=2.0, y=0.0, z=0.0)),
246 mu3d.rotate_z(square_rotation),
247 ]
248 )
249 )
252 GL.glColor3f(0.0, 0.0, 1.0)
253 GL.glBegin(GL.GL_QUADS)
254 for ms in square:
255 square_vector_ndc = mu3d.fn_stack.modelspace_to_ndc_fn()(ms)
256 GL.glVertex3f(
257 square_vector_ndc.x,
258 square_vector_ndc.y,
259 square_vector_ndc.z,
260 )
261 GL.glEnd()
Now we need to remove fns from the stack so that the lambda stack will convert from world space to NDC. This will allow us to just add the transformations from world space to paddle2 space on the stack.
265 mu3d.fn_stack.pop() # pop off square space to paddle 1 space
266 # current space is paddle 1 space
267 mu3d.fn_stack.pop() # # pop off paddle 1 model space to world space
268 # current space is world space
since paddle2’s modelspace is independent of paddle 1’s space, only leave the view and projection fns (1) - (4)
draw paddle 2¶
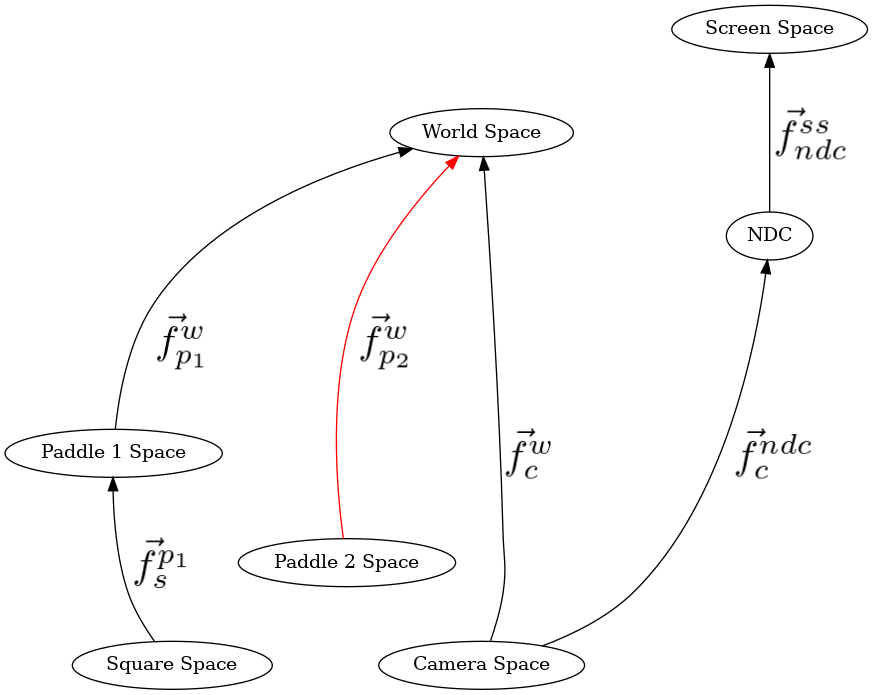
272 mu3d.fn_stack.push(
273 mu3d.compose(
274 [mu3d.translate(paddle2.position), mu3d.rotate_z(paddle2.rotation)]
275 )
276 )
280 # draw paddle 2
281 GL.glColor3f(*iter(paddle2.color))
282 GL.glBegin(GL.GL_QUADS)
283 for p2_v_ms in paddle2.vertices:
284 paddle2_vector_ndc = mu3d.fn_stack.modelspace_to_ndc_fn()(p2_v_ms)
285 GL.glVertex3f(
286 paddle2_vector_ndc.x,
287 paddle2_vector_ndc.y,
288 paddle2_vector_ndc.z,
289 )
290 GL.glEnd()
remove all fns from the function stack, as the next frame will set them clear makes the list empty, as the list (stack) will be repopulated the next iteration of the event loop.
294 # done rendering everything for this frame, just go ahead and clear all functions
295 # off of the stack, back to NDC as current space
296 mu3d.fn_stack.clear()
297
Swap buffers and execute another iteration of the event loop
301 glfw.swap_buffers(window)
Notice in the above code, adding functions to the stack is creating a shared context for transformations, and before we call “glVertex3f”, we always call “modelspace_to_ndc” on the modelspace vector. In Demo 19, we will be using OpenGL 2.1 matrix stacks. Although we don’t have the code for the OpenGL driver, given that you’ll see that we pass modelspace data directly to “glVertex3f”, it should be clear that the OpenGL implementation must fetch the modelspace to NDC transformations from the ModelView and Projection matrix stacks.