Camera Space - Demo 10¶
Objective¶
Graphical programs in which the viewer never “moves” are boring. Model a virtual “camera”, and let the user move the camera around in the scene. In this picture, notice that the purple paddle is no longer on the left side of the screen, but towards the right, horizontally.
Demo 10¶
How to Execute¶
Load src/modelviewprojection/demo10.py in Spyder and hit the play button.
Move the Paddles using the Keyboard¶
Keyboard Input |
Action |
|---|---|
w |
Move Left Paddle Up |
s |
Move Left Paddle Down |
k |
Move Right Paddle Down |
i |
Move Right Paddle Up |
d |
Increase Left Paddle’s Rotation |
a |
Decrease Left Paddle’s Rotation |
l |
Increase Right Paddle’s Rotation |
j |
Decrease Right Paddle’s Rotation |
UP |
Move the camera up, moving the objects down |
DOWN |
Move the camera down, moving the objects up |
LEFT |
Move the camera left, moving the objects right |
RIGHT |
Move the camera right, moving the objects left |
Description¶
“Camera space” means the coordinates of everything relative to a camera, not relative to world space.
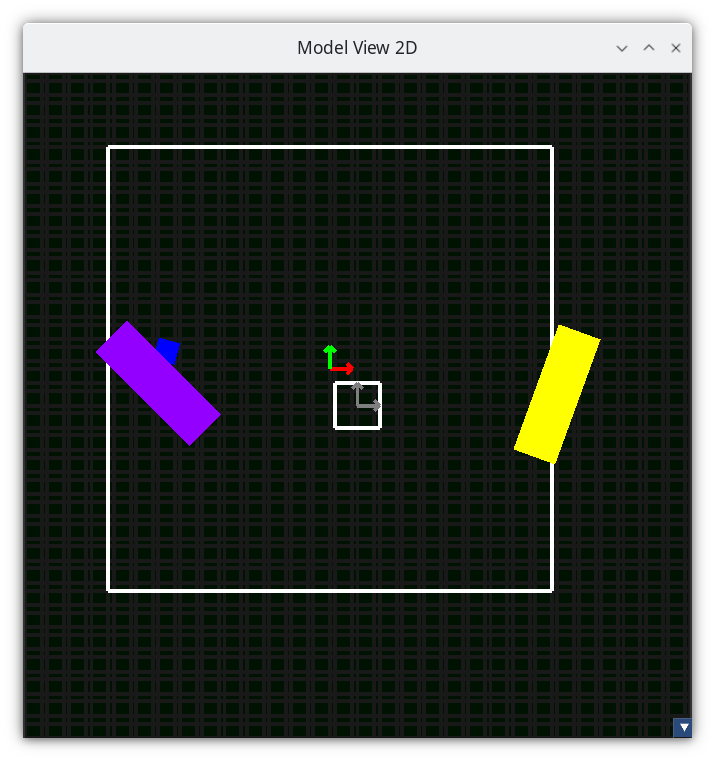
Camera space¶
In the picture above, NDC is the square in the center of the screen, and its coordinate system is defined by its two axes X and Y. The square to the to the left and up is the position of the camera; which has its own X axis and Y axis.
The coordinates of the paddle can be described in world space, or in camera space, and that we can create functions to convert coordinates between the two spaces.
Towards that, in the Cayley graph, camera space will be between world space and NDC, but which way should the direction of the edge be?
It could be
From world space to camera space.
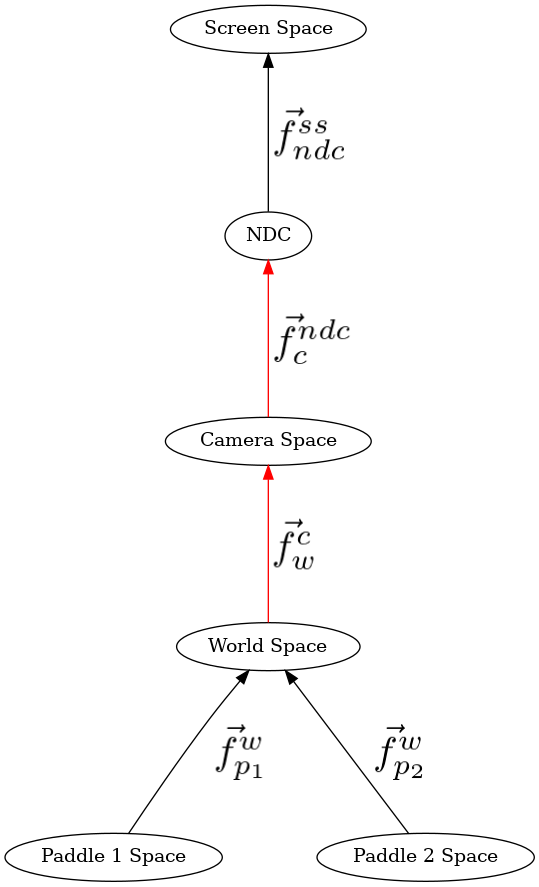
Demo 10¶
From camera space to world space.
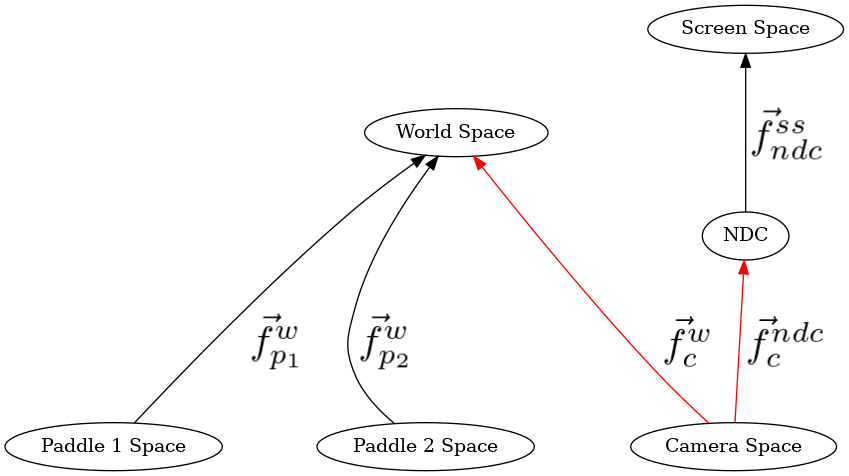
Demo 10¶
Since the camera’s position will be described relative to world space in world space coordinates, just like the paddles are, it makes more sense to use the latter, in which the directed edge goes from camera space to world space.
Think about it this way. Imagine you a driving. Are you staying in a constant position, and the wheels of your car rotate the entire earth and solar system around yourself? That’s one way to look at it, and the earth revolves around me too, but the mathematical descriptions of everything else that’s not you breaks down.
The math is easier in the aggregate if you describe your position as moving relative to earth.
But this introduces a new problem. Follow from the paddle’s modelspace to screen space. Up until this demo, we’ve always been following the the direction of each edges. In our new Cayley graph, when going from world space to camera space, we’re moving in the opposite direction of the edge.
Going against the direction of an edge in a Cayley Graph means that we don’t apply the function itself; instead we apply the inverse of the function. This concept comes from Group Theory in Abstract Algebra, the details of which won’t be discussed here, but we will use it to help us reason about the transformations.
Inverses¶
Inverse Of Translate¶
The inverse of
>>> v.translate(x,y)
is
>>> v.translate(-x,-y)
Inverse Of Rotate¶
The inverse of
>>> v.rotate(theta)
is
>>> v.rotate(-theta)
Inverse Of Scale¶
The inverse of
>>> v.scale(x,y)
is
>>> v.scale(1.0/x,1.0/y)
Inverse Of Sequence Of Functions¶
The inverse of a sequence of functions is the inverse of each function, applied in reverse order.
For the linear-algebra inclined reader,
The inverse of
>>> v.scale(x,y).translate(Vector(x,y))
is
>>> v.translate(-Vector(x,y).scale(1.0/x,1.0/y)
Think of the inverses this way. Stand up. Make sure that nothing is close around you that you could trip on or that you would walk into. Look forward. Keeping your eyes straight ahead, sidestep a few steps to the left. From your perspective, the objects in your room all moved to the right. Now, rotate your head to your right, keeping your eyes looking directly in front of your head. Which way did the room move? Towards the left.

Camera is 3D space¶
Looking at the graph paper on the ground there, that’s world space. The camera gets placed in world space just like any other modelspace data. In order to render from the camera’s point of view, we need to move and orient the -1.0 to 1.0 box relative to the camera to match the -1.0 to 1.0 box in world space.
Run “python mvpVisualization/modelviewperspectiveprojection/modelviewperspectiveprojection.py”, and follow along with the Cayley graph. The camera will be placed like any other modelspace data, but then the inverse of the transformations will be applied to all of the vertices.
For the attentive reader¶
The purpose of watching that animation was to see how the camera was placed just like the modelspace data was placed, while not modifying the modelspace data, but then the inverse was applied, moving the modelspace data.
The attentive reader may notice: “Bill, you said the the inverse causes the operations to be run in opposite order, yet I saw them run in the same order. For camera placement, I saw translate, then rotate sideways, then rotate up. For the inverse, I saw inverse translate, then inverse rotate sideways, then inverse rotate up. What gives?”
Well, the answer, which we talk about later in more detail, is that we change the order in which we read the sequence of transformations.
Let’s say we read the following from left to right
So we imagine the a transformation, then the b transformation, then the c.
To take the inverse, we reverse the order of the transformations, and invert them.
But now we read the transformations from right to left.
So we imagine the a inverse transformation, then the b inverse transformation, then the c inverse.
The author understands that this may be confusing to the reader, and seems illogical. Camera placement is, in the author’s opinion, the most difficult concept for a novice to grasp, and the author is unaware of a better explanation. Bear with the author, by the end of this book, it should make more sense to the reader.
Code¶
116
117
118@dataclasses.dataclass
119class Camera:
120 position_ws: mu2d.Vector2D = dataclasses.field(
121 default_factory=lambda: mu2d.Vector2D(x=0.0, y=0.0)
122 )
130def handle_inputs() -> None:
131 global camera
132
133 if glfw.get_key(window, glfw.KEY_UP) == glfw.PRESS:
134 camera.position_ws.y += 1.0
135 if glfw.get_key(window, glfw.KEY_DOWN) == glfw.PRESS:
136 camera.position_ws.y -= 1.0
137 if glfw.get_key(window, glfw.KEY_LEFT) == glfw.PRESS:
138 camera.position_ws.x -= 1.0
139 if glfw.get_key(window, glfw.KEY_RIGHT) == glfw.PRESS:
140 camera.position_ws.x += 1.0
...
The Event Loop¶
168while not glfw.window_should_close(window):
188 GL.glColor3f(*iter(paddle1.color))
189
190 GL.glBegin(GL.GL_QUADS)
191 for p1_v_ms in paddle1.vertices:
192 ms_to_ws: mu2d.InvertibleFunction = mu2d.compose(
193 [mu2d.translate(paddle1.position), mu2d.rotate(paddle1.rotation)]
194 )
195 paddle1_vector_ws: mu2d.Vector2D = ms_to_ws(p1_v_ms)
196
197 ws_to_cs: mu2d.InvertibleFunction = mu2d.inverse(
198 mu2d.translate(camera.position_ws)
199 )
200 paddle1_vector_cs: mu2d.Vector2D = ws_to_cs(paddle1_vector_ws)
201
202 cs_to_ndc: mu2d.InvertibleFunction = mu2d.uniform_scale(1.0 / 10.0)
203 paddle1_vector_ndc: mu2d.Vector2D = cs_to_ndc(paddle1_vector_cs)
204
205 GL.glVertex2f(paddle1_vector_ndc.x, paddle1_vector_ndc.y)
206 GL.glEnd()
The camera’s position is at camera.x, camera.y. So apply the inverse of the camera’s transformations to paddle 1’s vertices, i.e. translate with the negative values.
210 GL.glColor3f(*iter(paddle2.color))
211
212 GL.glBegin(GL.GL_QUADS)
213 for p2_v_ms in paddle2.vertices:
214 ms_to_ndc: mu2d.InvertibleFunction = mu2d.compose(
215 [
216 # camera space to NDC
217 mu2d.uniform_scale(1.0 / 10.0),
218 # world space to camera space
219 mu2d.inverse(mu2d.translate(camera.position_ws)),
220 # model space to world space
221 mu2d.compose(
222 [
223 mu2d.translate(paddle2.position),
224 mu2d.rotate(paddle2.rotation),
225 ]
226 ),
227 ]
228 )
229
230 paddle2_vector_ndc: mu2d.Vector2D = ms_to_ndc(p2_v_ms)
231
232 GL.glVertex2f(paddle2_vector_ndc.x, paddle2_vector_ndc.y)
233 GL.glEnd()
The camera’s position is at camera.x, camera.y. So apply the inverse of the camera’s transformations to paddle 2’s vertices, i.e. translate with the negative values.