3D Perspective - Demo 18¶
Objective¶
Implement a perspective projection so that objects further away are smaller than the would be if they were close by
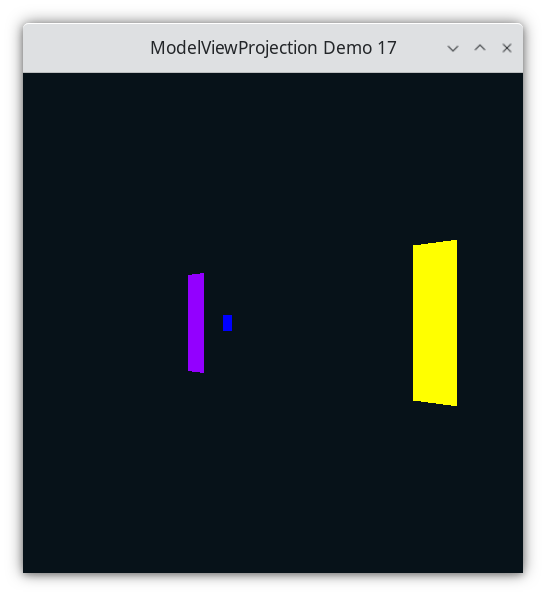
Demo 17¶
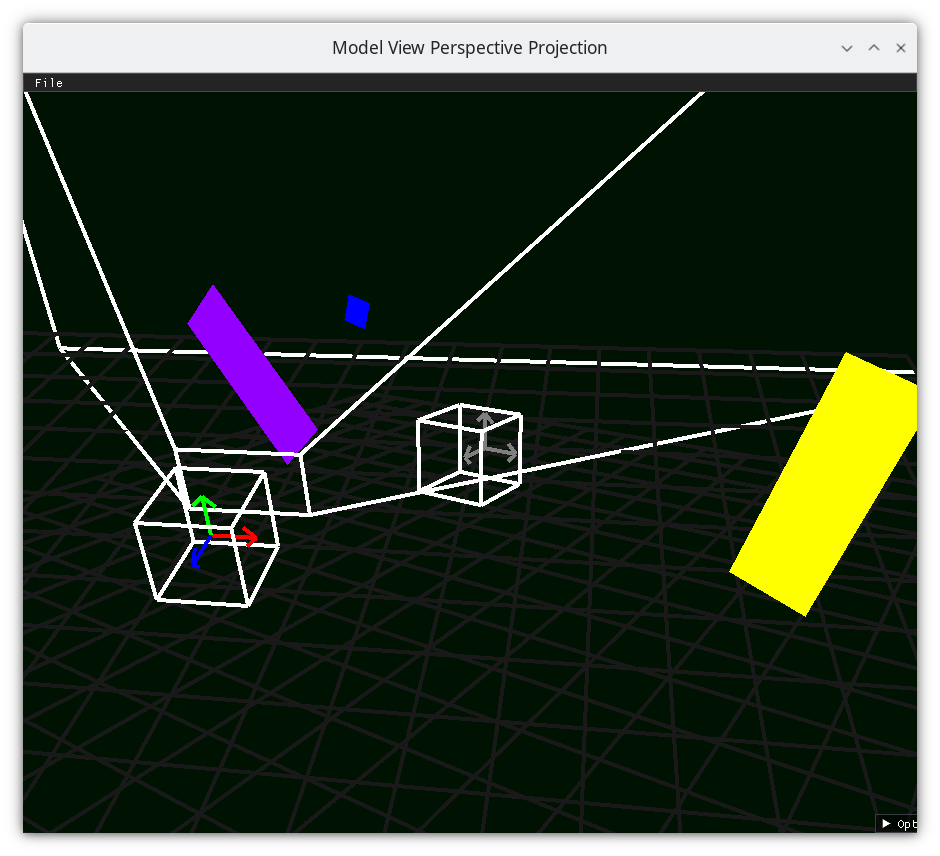
Frustum 1¶
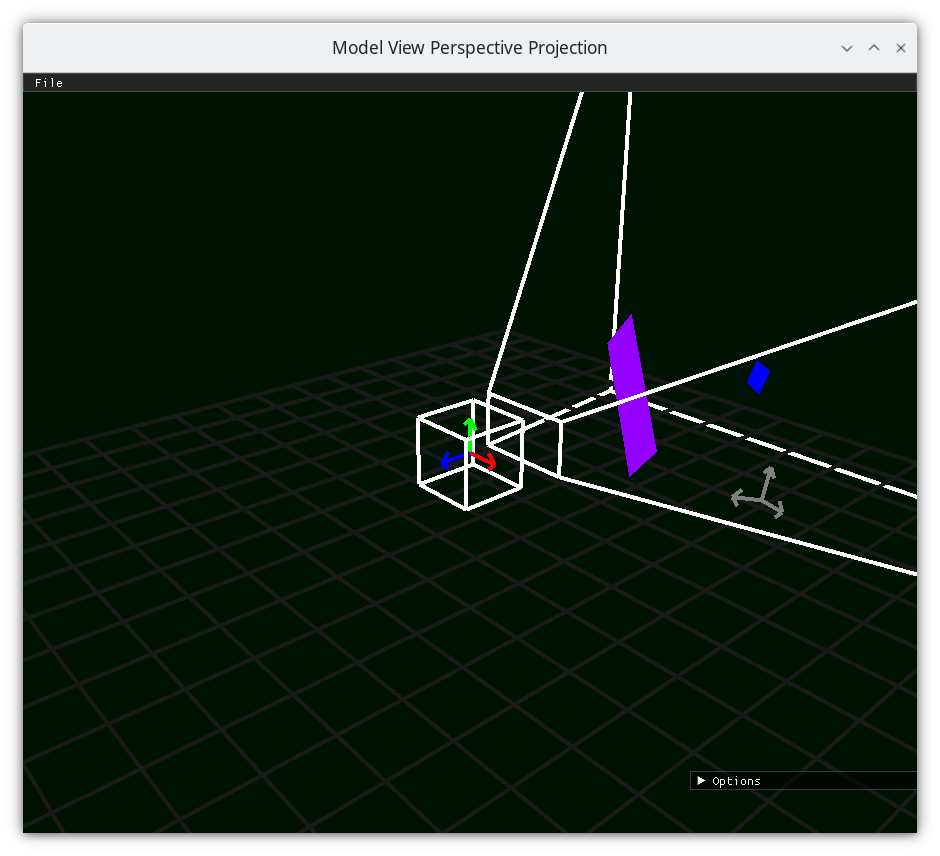
Frustum 2¶
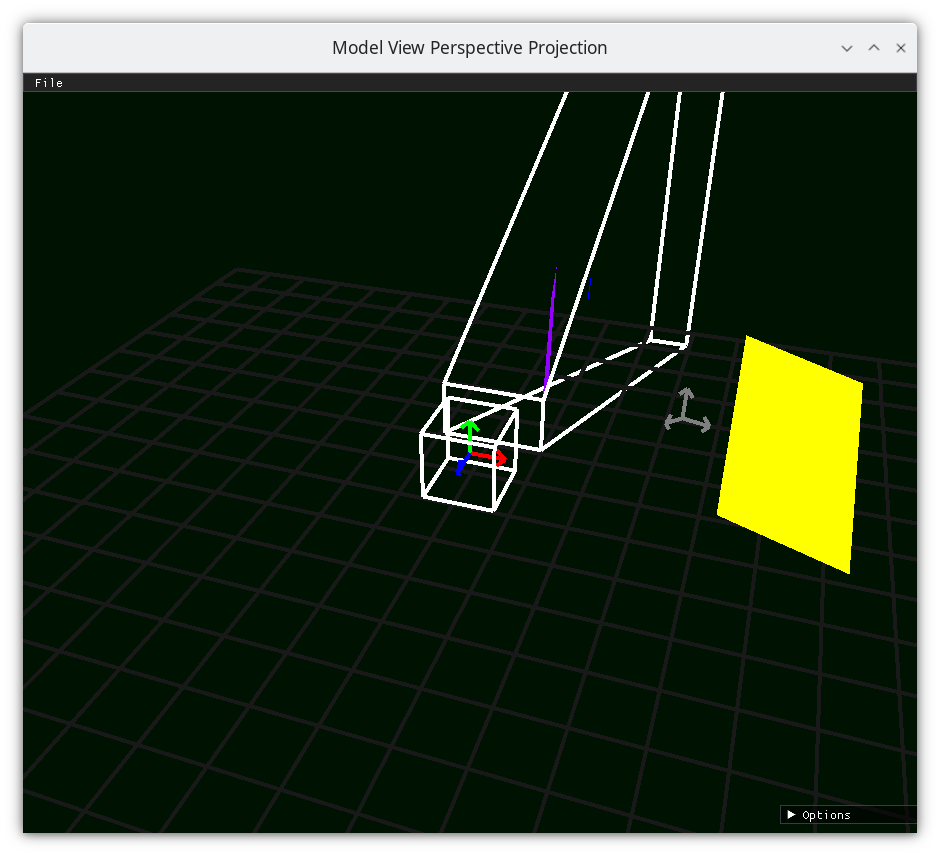
Frustum 3¶
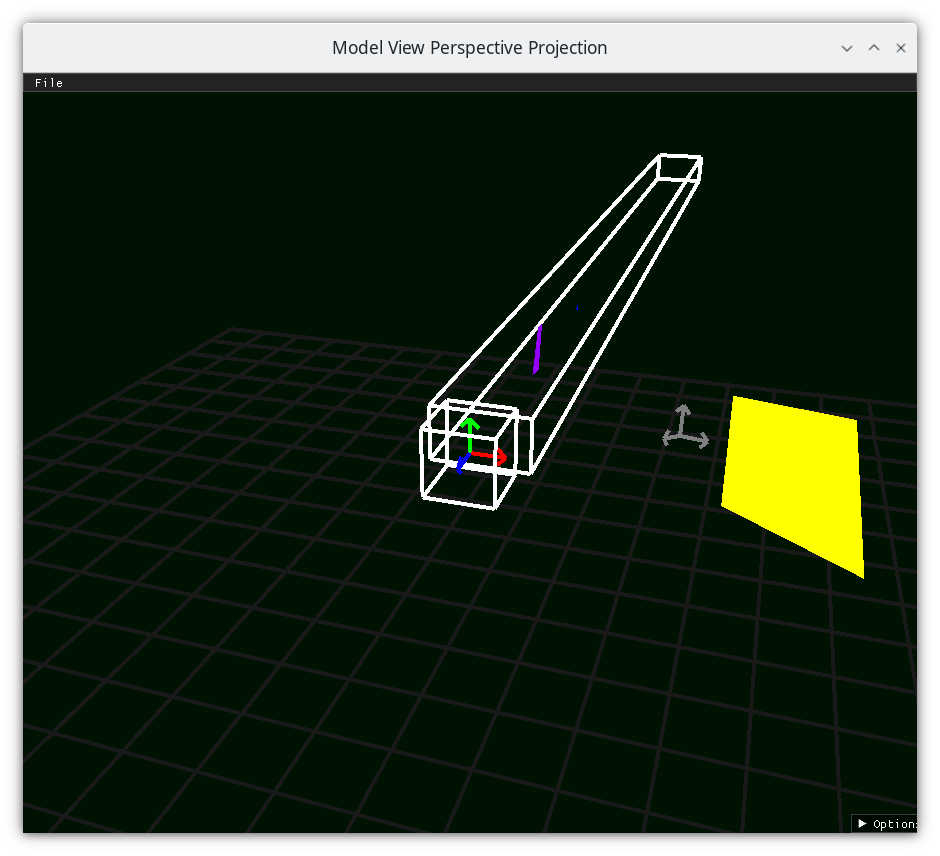
Frustum 4¶
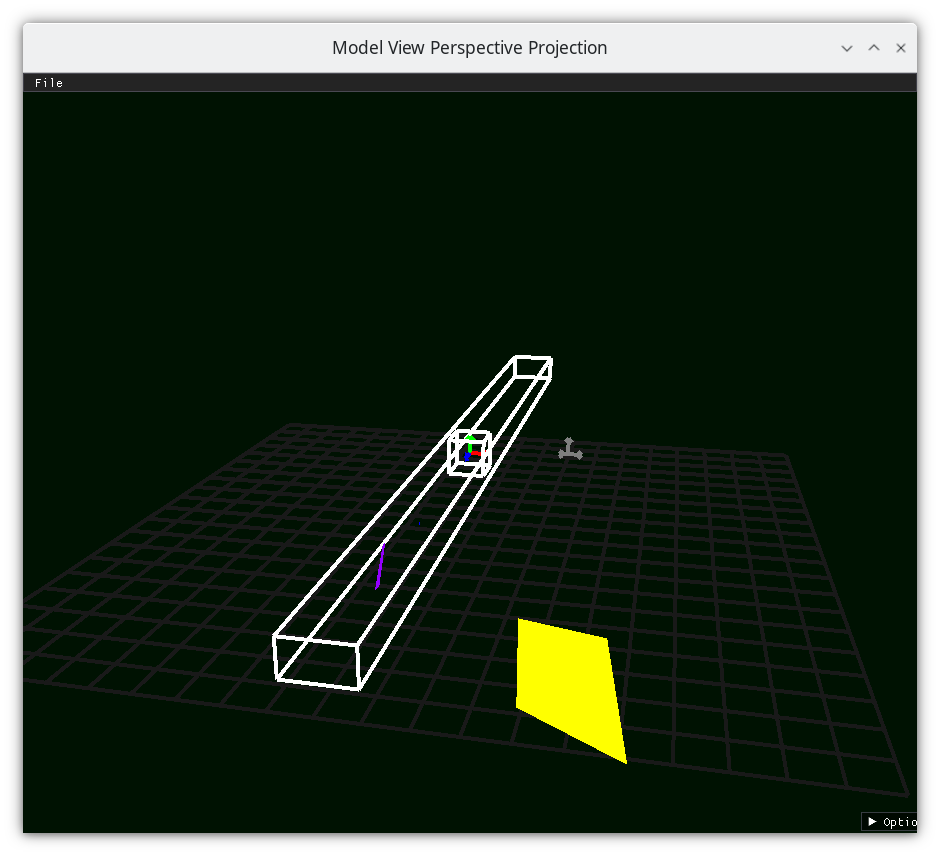
Frustum 5¶
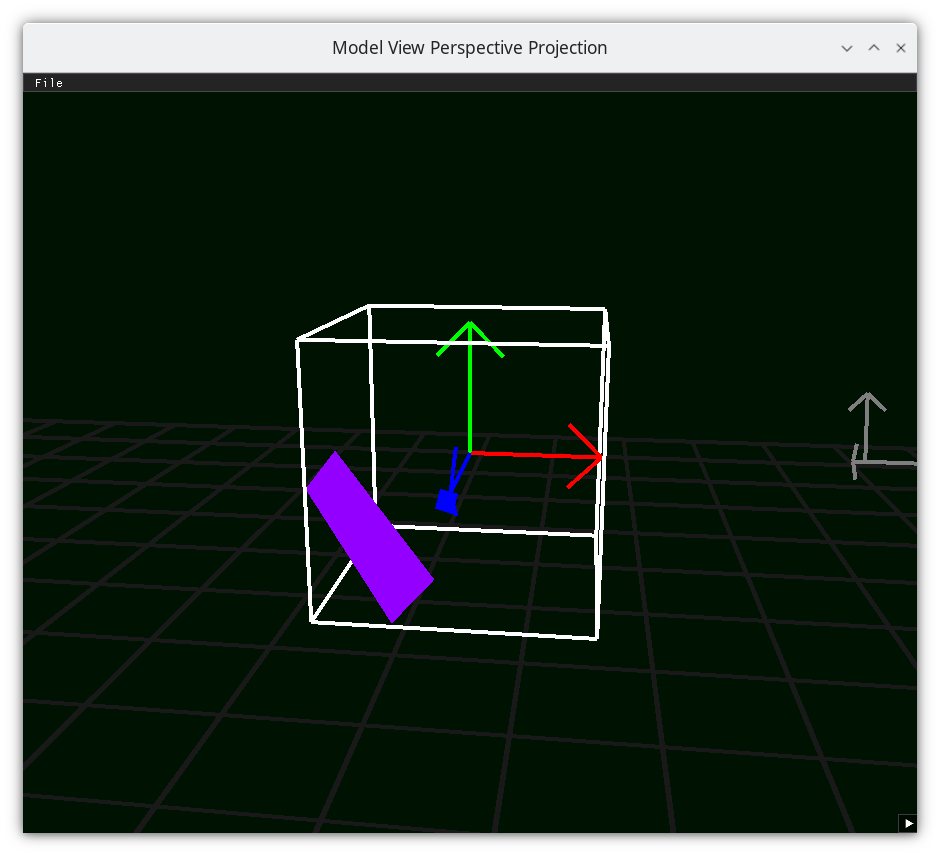
Frustum 6¶
How to Execute¶
Load src/modelviewprojection/demo18.py in Spyder and hit the play button.
Move the Paddles using the Keyboard¶
Keyboard Input |
Action |
|---|---|
w |
Move Left Paddle Up |
s |
Move Left Paddle Down |
k |
Move Right Paddle Down |
i |
Move Right Paddle Up |
d |
Increase Left Paddle’s Rotation |
a |
Decrease Left Paddle’s Rotation |
l |
Increase Right Paddle’s Rotation |
j |
Decrease Right Paddle’s Rotation |
UP |
Move the camera up, moving the objects down |
DOWN |
Move the camera down, moving the objects up |
LEFT |
Move the camera left, moving the objects right |
RIGHT |
Move the camera right, moving the objects left |
q |
Rotate the square around its center |
e |
Rotate the square around paddle 1’s center |
Description¶
------------------------------- far z
\ | /
\ | /
\ (x,z) *----|(0,z) /
\ | | /
\ | | /
\ | | /
\ | | /
\ | | /
\ | | /
\---*-------- near z
| | /
|\ | /
| \ | /
| \ | /
| \|/
-----------------*----*-(0,0)-------------------
(x,0)
If we draw a straight line between (x,z) and (0,0), we will have a right triangle with vertices (0,0), (0,z), and (x,z).
There also will be a similar right triangle with vertices (0,0), (0,nearZ), and whatever point the line above intersects the line at z=nearZ. Let’s call that point (projX, nearZ)
because right angle and tan(theta) = tan(theta)
x / z = projX / nearZ
projX = x / z * nearZ
So use projX as the transformed x value, and keep the distance z.
----------- far z
| |
| |
(x / z * nearZ,z) * | non-linear -- the transformation of x depends on its z value
| |
| |
| |
| |
| |
| |
| |
| |
------------ near z
\ | /
\ | /
\ | /
\ | /
\|/
----------------------*-(0,0)-------------------
Top calculation based off of vertical field of view
/* top
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
origin/ |
/ fov/2 |
z----*---------------*
|\ |-nearZ
| \ |
| \ |
x \ |
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\|
Right calculation based off of Top and aspect ration
top
-------------------------------------------------------
| |
| y |
| | |
| | |
| *----x | right =
| origin | top * aspectRatio
| |
| | aspect ratio should be the viewport's
| | width/height, not necessarily the
------------------------------------------------------- window's
61@dataclasses.dataclass
62class Vector3D(mu2d.Vector2D):
63 z: float #: The z-component of the 3D Vector
...
199def perspective(
200 field_of_view: float, aspect_ratio: float, near_z: float, far_z: float
201) -> mu.InvertibleFunction:
202 # field_of_view, dataclasses.field of view, is angle of y
203 # aspect_ratio is x_width / y_width
204
205 top: float = -near_z * math.tan(math.radians(field_of_view) / 2.0)
206 right: float = top * aspect_ratio
207
208 fn = ortho(
209 left=-right,
210 right=right,
211 bottom=-top,
212 top=top,
213 near=near_z,
214 far=far_z,
215 )
216
217 def f(vector: mu.Vector) -> mu.Vector:
218 assert isinstance(vector, Vector3D)
219 s1d: mu.InvertibleFunction = mu.uniform_scale(near_z / vector.z)
220 x_component: mu.Vector = s1d(mu1d.Vector1D(x=vector.x))
221 y_component: mu.Vector = s1d(mu1d.Vector1D(x=vector.y))
222 assert isinstance(x_component, mu1d.Vector1D)
223 assert isinstance(y_component, mu1d.Vector1D)
224
225 rectangular_prism: Vector3D = Vector3D(
226 x=x_component.x, y=y_component.x, z=vector.z
227 )
228 return fn(rectangular_prism)
229
230 def f_inv(vector: mu.Vector) -> mu.Vector:
231 assert isinstance(vector, Vector3D)
232 rectangular_prism: mu.Vector = mu.inverse(fn)(vector)
233 assert isinstance(rectangular_prism, Vector3D)
234
235 inverse_s1d: mu.InvertibleFunction = mu.inverse(
236 mu.uniform_scale(near_z / vector.z)
237 )
238 x_component: mu.Vector = inverse_s1d(
239 mu1d.Vector1D(x=rectangular_prism.x)
240 )
241 y_component: mu.Vector = inverse_s1d(
242 mu1d.Vector1D(x=rectangular_prism.y)
243 )
244 assert isinstance(x_component, mu1d.Vector1D)
245 assert isinstance(y_component, mu1d.Vector1D)
246
247 return Vector3D(
248 x_component.x,
249 y_component.x,
250 rectangular_prism.z,
251 )
252
253 return mu.InvertibleFunction(f, f_inv)
202while not glfw.window_should_close(window):
...
244 # cameraspace to NDC
245 with mu3d.push_transformation(
246 mu3d.perspective(
247 field_of_view=45.0, aspect_ratio=1.0, near_z=-0.1, far_z=-1000.0
248 )
249 ):
250 # world space to camera space, which is mu3d.inverse of camera space to
251 # world space
252 with mu3d.push_transformation(
253 mu3d.inverse(
254 mu3d.compose(
255 [
256 mu3d.translate(camera.position_ws),
257 mu3d.rotate_y(camera.rot_y),
258 mu3d.rotate_x(camera.rot_x),
259 ]
260 )
261 )
262 ):
263 # paddle 1 space to world space
264 with mu3d.push_transformation(
265 mu3d.compose(
266 [
267 mu3d.translate(paddle1.position),
268 mu3d.rotate_z(paddle1.rotation),
269 ]
270 )
271 ):
272 GL.glColor3f(*iter(paddle1.color))
273 GL.glBegin(GL.GL_QUADS)
274 for p1_v_ms in paddle1.vertices:
275 paddle1_vector_ndc = mu3d.fn_stack.modelspace_to_ndc_fn()(
276 p1_v_ms
277 )
278 GL.glVertex3f(
279 paddle1_vector_ndc.x,
280 paddle1_vector_ndc.y,
281 paddle1_vector_ndc.z,
282 )
283 GL.glEnd()