Adding Depth - Z axis Demo 14¶
Purpose¶
Do the same stuff as the previous demo, but use 3D coordinates, where the negative z axis goes into the screen (because of the right hand rule). Positive z comes out of the monitor towards your face.
Things that this demo doesn’t end up doing correctly:
The blue square is always drawn, even when its z-coordinate in world space is less than the paddle’s. The solution will be z-buffering https://en.wikipedia.org/wiki/Z-buffering, and it is implemented in the next demo.
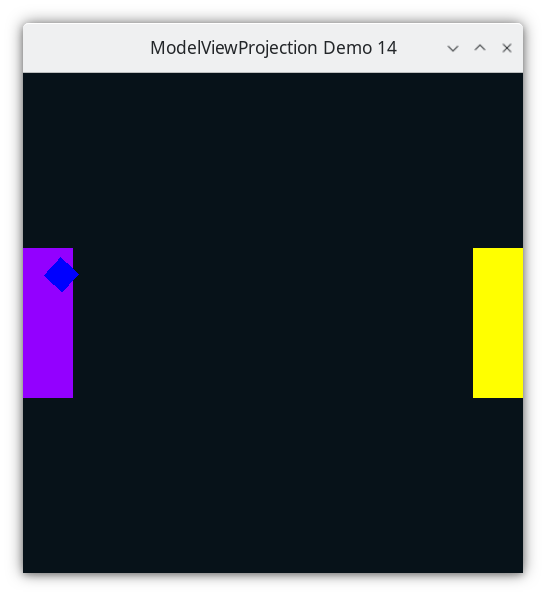
Demo 14¶
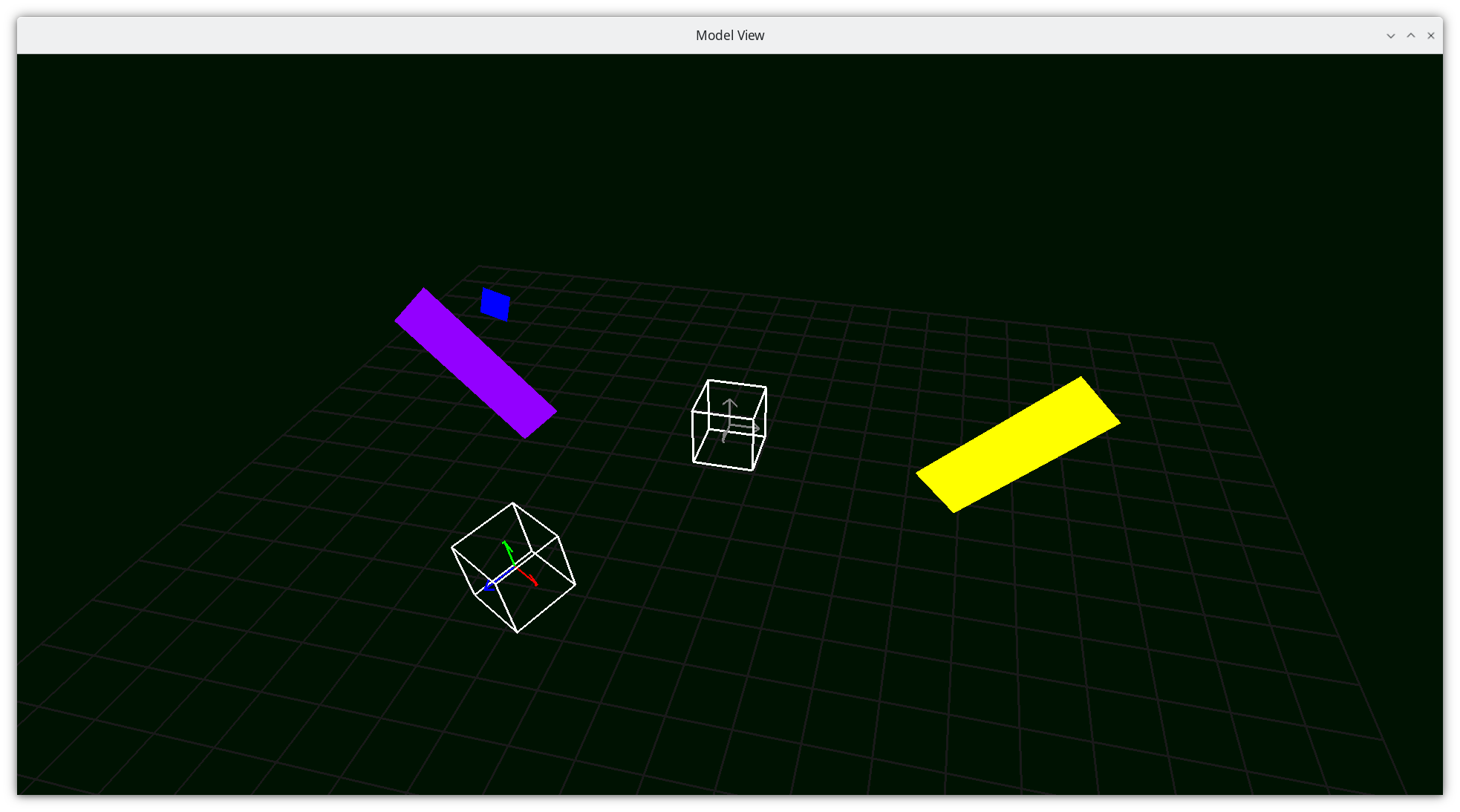
Camera Space¶
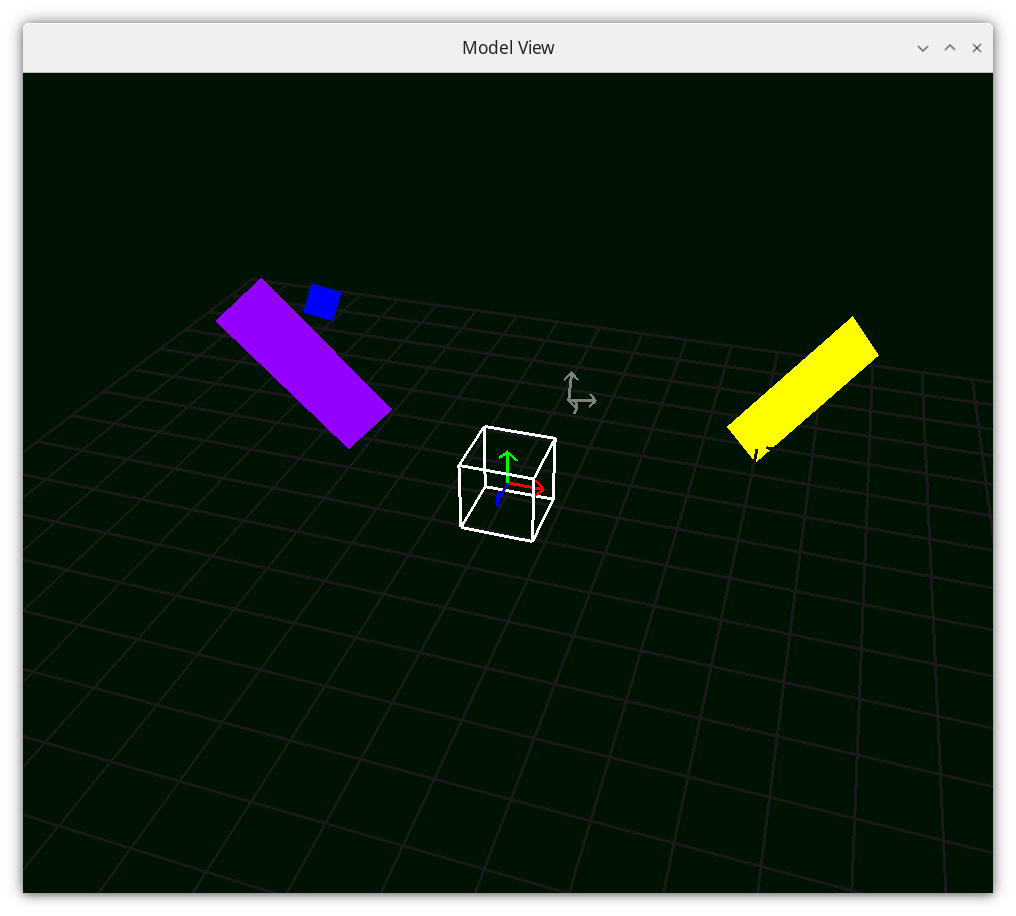
Camera Space¶
How to Execute¶
Load src/demo14/demo.py in Spyder and hit the play button
Move the Paddles using the Keyboard¶
Keyboard Input |
Action |
|---|---|
w |
Move Left Paddle Up |
s |
Move Left Paddle Down |
k |
Move Right Paddle Down |
i |
Move Right Paddle Up |
d |
Increase Left Paddle’s Rotation |
a |
Decrease Left Paddle’s Rotation |
l |
Increase Right Paddle’s Rotation |
j |
Decrease Right Paddle’s Rotation |
UP |
Move the camera up, moving the objects down |
DOWN |
Move the camera down, moving the objects up |
LEFT |
Move the camera left, moving the objects right |
RIGHT |
Move the camera right, moving the objects left |
q |
Rotate the square around its center |
e |
Rotate the square around paddle 1’s center |
Description¶
Vertex data will now have an X, Y, and Z component.
Rotations around an angle in 3D space follow the right hand rule. Here’s a link to them in matrix form, which we have not yet covered.
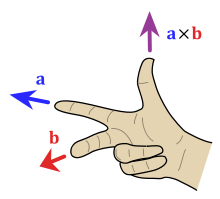
With open palm, fingers on the x axis, rotating the fingers to y axis, means that the positive z axis is in the direction of the thumb. Positive Theta moves in the direction that your fingers did.
starting on the y axis, rotating to z axis, thumb is on the positive x axis.
starting on the z axis, rotating to x axis, thumb is on the positive y axis.
109@dataclass
110class Vertex2D:
111 x: float
112 y: float
113
114 def __add__(self, rhs: Vertex2D) -> Vertex2D:
115 return Vertex2D(x=self.x + rhs.x, y=self.y + rhs.y)
116
117 def translate(self: Vertex2D, translate_amount: Vertex2D) -> Vertex2D:
118 return self + translate_amount
119
120 def __mul__(self, scalar: float) -> Vertex2D:
121 return Vertex2D(x=self.x * scalar, y=self.y * scalar)
122
123 def __rmul__(self, scalar: float) -> Vertex2D:
124 return self * scalar
125
126 def uniform_scale(self: Vertex2D, scalar: float) -> Vertex2D:
127 return self * scalar
128
129 def scale(self: Vertex2D, scale_x: float, scale_y: float) -> Vertex2D:
130 return Vertex2D(x=self.x * scale_x, y=self.y * scale_y)
131
132 def __neg__(self):
133 return -1.0 * self
134
135 def rotate_90_degrees(self: Vertex2D):
136 return Vertex2D(x=-self.y, y=self.x)
137
138 def rotate(self: Vertex2D, angle_in_radians: float) -> Vertex2D:
139 return (
140 math.cos(angle_in_radians) * self
141 + math.sin(angle_in_radians) * self.rotate_90_degrees()
142 )
143
144
145@dataclass
146class Vertex:
147 x: float
148 y: float
149 z: float
150
151 def __add__(self, rhs: Vertex) -> Vertex:
152 return Vertex(x=self.x + rhs.x, y=self.y + rhs.y, z=self.z + rhs.z)
153
154 def translate(self: Vertex, translate_amount: Vertex) -> Vertex:
155 return self + translate_amount
156
Rotate Z¶
Rotate Z is the same rotate that we’ve used so far, but doesn’t affect the z component at all.
174 def rotate_z(self: Vertex, angle_in_radians: float) -> Vertex:
175 xy_on_xy: Vertex2D = Vertex2D(x=self.x, y=self.y).rotate(angle_in_radians)
176 return Vertex(x=xy_on_xy.x, y=xy_on_xy.y, z=self.z)
177
Rotate X¶
160 def rotate_x(self: Vertex, angle_in_radians: float) -> Vertex:
161 yz_on_xy: Vertex2D = Vertex2D(x=self.y, y=self.z).rotate(angle_in_radians)
162 return Vertex(x=self.x, y=yz_on_xy.x, z=yz_on_xy.y)
163
Rotate Y¶
167 def rotate_y(self: Vertex, angle_in_radians: float) -> Vertex:
168 zx_on_xy: Vertex2D = Vertex2D(x=self.z, y=self.x).rotate(angle_in_radians)
169 return Vertex(x=zx_on_xy.y, y=self.y, z=zx_on_xy.y)
170
Scale¶
181
182 def __mul__(self, scalar: float) -> Vertex:
183 return Vertex(x=self.x * scalar, y=self.y * scalar, z=self.z * scalar)
184
185 def __rmul__(self, scalar: float) -> Vertex:
186 return self * scalar
187
188 def uniform_scale(self: Vertex, scalar: float) -> Vertex:
189 return self * scalar
190
191 def scale(self: Vertex, scale_x: float, scale_y: float, scale_z: float) -> Vertex:
192 return Vertex(x=self.x * scale_x, y=self.y * scale_y, z=self.z * scale_z)
193
194 def __neg__(self):
195 return -1.0 * self
196
Code¶
The only new aspect of the code below is that the paddles have a z-coordinate of 0 in their modelspace.
211paddle1: Paddle = Paddle(
212 vertices=[
213 Vertex(x=-1.0, y=-3.0, z=0.0),
214 Vertex(x=1.0, y=-3.0, z=0.0),
215 Vertex(x=1.0, y=3.0, z=0.0),
216 Vertex(x=-1.0, y=3.0, z=0.0),
217 ],
218 r=0.578123,
219 g=0.0,
220 b=1.0,
221 position=Vertex(x=-9.0, y=0.0, z=0.0),
222)
223
224paddle2: Paddle = Paddle(
225 vertices=[
226 Vertex(x=-1.0, y=-3.0, z=0.0),
227 Vertex(x=1.0, y=-3.0, z=0.0),
228 Vertex(x=1.0, y=3.0, z=0.0),
229 Vertex(x=-1.0, y=3.0, z=0.0),
230 ],
231 r=1.0,
232 g=1.0,
233 b=0.0,
234 position=Vertex(x=9.0, y=0.0, z=0.0),
235)
The only new aspect of the square below is that the paddles have a z-coordinate of 0 in their modelspace. N.B that since we do a sequence transformations to the modelspace data to get to world-space coordinates, the X, Y, and Z coordinates are subject to be different.
240@dataclass
241class Camera:
242 position_ws: Vertex = field(default_factory=lambda: Vertex(x=0.0, y=0.0, z=0.0))
243
244
245camera: Camera = Camera()
The camera now has a z-coordinate of 0 also.
249square: list[Vertex] = [
250 Vertex(x=-0.5, y=-0.5, z=0.0),
251 Vertex(x=0.5, y=-0.5, z=0.0),
252 Vertex(x=0.5, y=0.5, z=0.0),
253 Vertex(x=-0.5, y=0.5, z=0.0),
254]
Event Loop¶
307while not glfw.window_should_close(window):
...
Draw Paddle 1
326 glColor3f(paddle1.r, paddle1.g, paddle1.b)
327 glBegin(GL_QUADS)
328 for paddle1_vertex_ms in paddle1.vertices:
329 paddle1_vertex_ws: Vertex = paddle1_vertex_ms.rotate_z(
330 paddle1.rotation
331 ).translate(paddle1.position)
332 paddle1_vertex_cs: Vertex = paddle1_vertex_ws.translate(-camera.position_ws)
333 paddle1_vertex_ndc: Vertex = paddle1_vertex_cs.uniform_scale(scalar=1.0 / 10.0)
334 glVertex2f(paddle1_vertex_ndc.x, paddle1_vertex_ndc.y)
335 glEnd()
The square should not be visible when hidden behind the paddle1, as we do a translate by -1. But in running the demo, you see that the square is always drawn over the paddle.
Draw the Square
339 # draw square
340 glColor3f(0.0, 0.0, 1.0)
341 glBegin(GL_QUADS)
342 for model_space in square:
343 paddle_1_space: Vertex = (
344 model_space.rotate_z(square_rotation)
345 .translate(Vertex(x=2.0, y=0.0, z=0.0))
346 .rotate_z(rotation_around_paddle1)
347 .translate(Vertex(x=0.0, y=0.0, z=-1.0))
348 )
349 world_space: Vertex = paddle_1_space.rotate_z(paddle1.rotation).translate(
350 paddle1.position
351 )
352 camera_space: Vertex = world_space.translate(-camera.position_ws)
353 ndc: Vertex = camera_space.uniform_scale(scalar=1.0 / 10.0)
354 glVertex3f(ndc.x, ndc.y, ndc.z)
355 glEnd()
This is because without depth buffering, the object drawn last clobbers the color of any previously drawn object at the pixel. Try moving the square drawing code to the beginning, and you will see that the square can be hidden behind the paddle.
Draw Paddle 2
359 # draw paddle 2
360 glColor3f(paddle2.r, paddle2.g, paddle2.b)
361 glBegin(GL_QUADS)
362 for paddle2_vertex_ms in paddle2.vertices:
363 paddle2_vertex_ws: Vertex = paddle2_vertex_ms.rotate_z(
364 paddle2.rotation
365 ).translate(paddle2.position)
366 paddle2_vertex_cs: Vertex = paddle2_vertex_ws.translate(-camera.position_ws)
367 paddle2_vertex_ndc: Vertex = paddle2_vertex_cs.uniform_scale(scalar=1.0 / 10.0)
368 glVertex3f(paddle2_vertex_ndc.x, paddle2_vertex_ndc.y, paddle2_vertex_ndc.z)
369 glEnd()
Added translate in 3D. Added scale in 3D. These are just like the 2D versions, just with the same process applied to the z axis.
They direction of the rotation is defined by the right hand rule.